Chapitre 2 Tests basés sur la fonction de répartition empirique et sur les rangs
Les slides associés à ce chapitre sont disponibles ici
2.1 Rappels
2.1.1 Fonction de répartition et quantiles
Soit \(X\) une v.a.r de fonction de répartition \(F\). On rappelle que, pour tout \(t\in \mathbb{R}\), \[ F(t) = \mathbb{P}(X\leq t). \]
Definition 2.1 Soit \(F\) une fonction de répartition. On définit la fonction quantile (ou inverse généralisée) \(F^{-1}\) de \(F\) par \[ \forall p \in [0,1],\ F^{-1}(p) = \mbox{inf} \left\{t\in \mathbb{R};\ F(t) \geq p \right\}. \]
Remark. Si \(F\) est une bijection, \(F^{-1}\) est la bijection réciproque.
Exercise 2.1 Calculez \(F^{-1}\) pour la loi de Bernoulli de paramètre \(\theta\).
Proposition 2.1 Soit \(t\in\mathbb{R}\) et \(p_0\in]0,1[\).
- \(F\) est croissante, continue à droite, \(\underset{t\rightarrow -\infty}{\lim}F(t)=0\), \(\underset{t\rightarrow +\infty}{\lim}F(t)=1\).
- \(\{t\in\mathbb{R};\ F(t)\geq p_0\} = [F^{-1}(p_0), +\infty[\)
- \(F^{-1}\) est croissante
- \(F\circ F^{-1}(p_0)\geq p_0\) avec égalité si \(p_0\in F(\mathbb{R})\).
- \(F(t)\geq p_0 \Leftrightarrow t \geq F^{-1}(p_0)\)
- Si \(U\sim\mathcal{U}([0,1])\), \(F^{-1}(U)\) a pour fonction de répartition \(F\).
2.1.2 Fonction de répartition empirique
Soit \(X_1,X_2, \ldots X_n\) une suite de variables aléatoires réelles i.i.d. de fonction de répartition \(F\).
Definition 2.2 On appelle fonction de répartition empirique associée au \(n\)-échantillon \((X_1,X_2, \ldots X_n)\) la fonction \[ \hat{F}_n(t)=\frac 1n \sum_{i=1}^n \mathbb{1}_{X_i \leq t}. \]
Remark. La fonction de répartition empirique de l’échantillon \((X_1,\ldots,X_n)\) s’exprime également à partir des statistiques d’ordre \(X_{(1)}\leq X_{(2)}\leq \ldots\leq X_{(n)}\) : \[ \hat{F}_n(t)=\frac 1n \sum_{i=1}^n \mathbb{1}_{X_{(i)} \leq t} \] ce qui permet de tracer facilement son graphique (voir Figure 2.1).
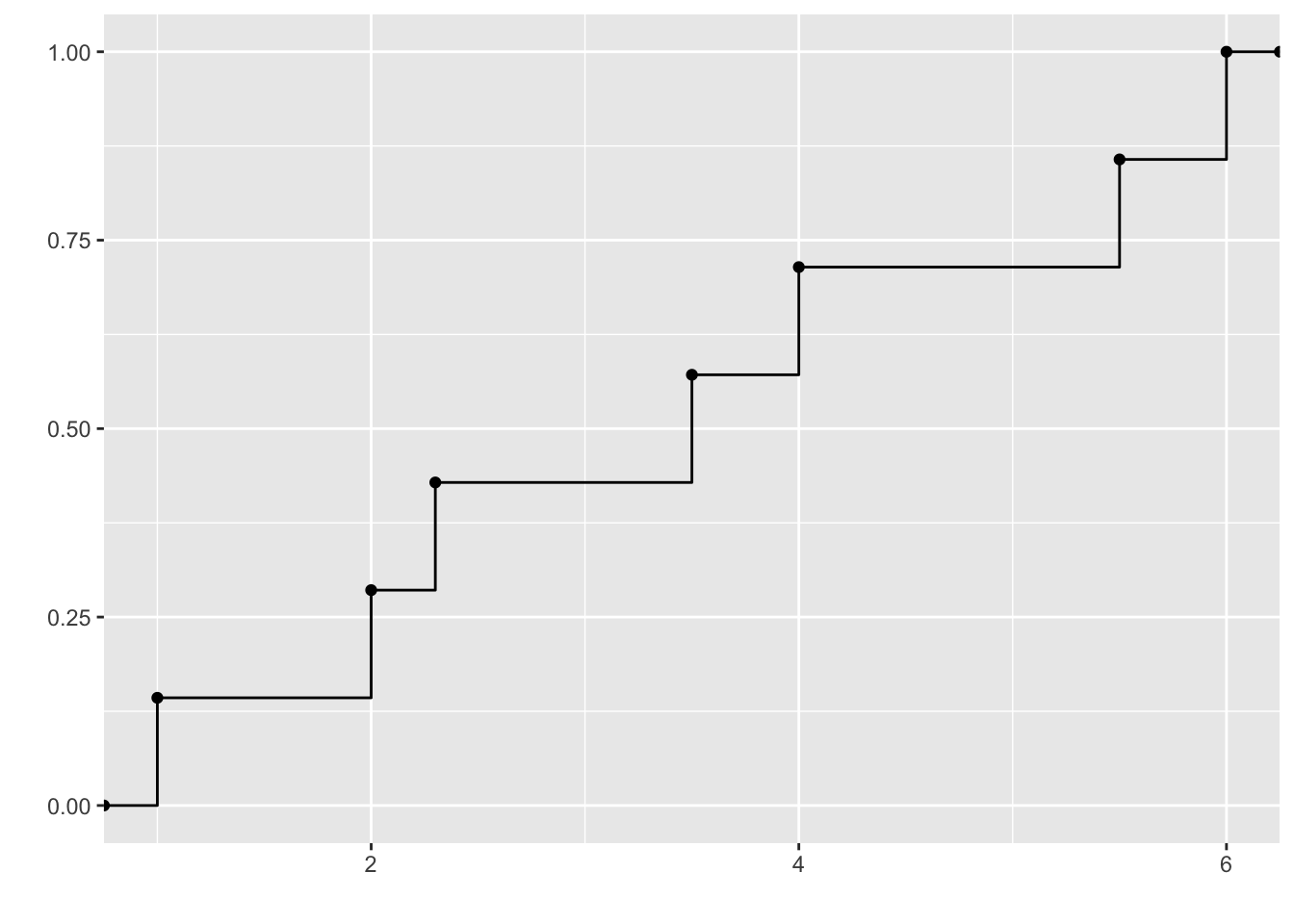
Figure 2.1: Fonction de répartition empirique pour l’échantillon observé (2, 3.5, 1, 4, 2.3, 6, 5.5)
Rappelons quelques propriétés de la fonction de répartition empirique.
Proposition 2.2 Propriétés de la fonction \(\hat{F}_n(.)\)
- \(\hat{F}_n\) est croissante, continue à droite, \(\underset{t\rightarrow -\infty}{\lim}\hat{F}_n(t)=0\), \(\underset{t\rightarrow +\infty}{\lim}\hat F_n(t)=1\).
- Pour tout \(t\in\mathbb{R}\), \(n \hat{F}_n(t)\) suit une loi binomiale de paramètre \((n, F(t))\).
- Pour tout \(t\in\mathbb{R}\), \(\hat{F}_n(t)\) est un estimateur sans biais de \(F(t)\).
- Pour tout \(t\in\mathbb{R}\) \[ \mbox{Var}(\hat{F}_n(t))=\frac{F(t)(1-F(t))}{n} \underset{n\rightarrow +\infty}{\longrightarrow} 0.\]
- Pour tout \(t\in\mathbb{R}\), \(\hat{F}_n(t) \underset{n\rightarrow+\infty}{\stackrel{\mathbb{P}}{\longrightarrow}}F(t)\)
- On déduit du TLC que pour tout \(t\in\mathbb{R}\) tel que \(F(t)(1-F(t))\neq 0\), \[\sqrt{n} (\hat F_n(t)-F(t)) \underset{n\rightarrow+\infty}{\stackrel{\mathcal L}{\longrightarrow}} \mathcal{N} (0, F(t)(1-F(t))).\]
- Glivenko-Cantelli (admis) \[ \underset{t\in\mathbb{R}}{\sup}\ | \hat F_n(t) - F(t) | \underset{n \rightarrow +\infty}{\stackrel{p.s}{\longrightarrow}} 0. \]
2.2 Test de Kolmogorov de comparaison ou d’adéquation
Soit \(X_1, \ldots , X_n\) des v.a.r i.i.d. de même loi que \(X\), de fonction de répartition \(F\) supposée continue. On se donne une fonction de répartition \(F_0\) supposée continue sur \(\mathbb{R}\) et \(Y_0\) une v.a.r de fonction de répartition \(F_0\).
On souhaite construire un test de \(\mathcal{H}_0\): “\(X\) et \(Y_0\) ont la même loi (\(F=F_0\))” contre :
- \(\mathcal{H}_1\) : \(X\) et \(Y_0\) ne suivent pas la même loi (\(F\neq F_0\))
- \(\mathcal{H}_1^{+}\) : \(X\) a tendance à prendre des valeurs plus petites que \(Y_0\) (\(F \geq F_0\))
- \(\mathcal{H}_1^{-}\) : \(X\) a tendance à prendre des valeurs plus grandes que \(Y_0\) (\(F \leq F_0\))
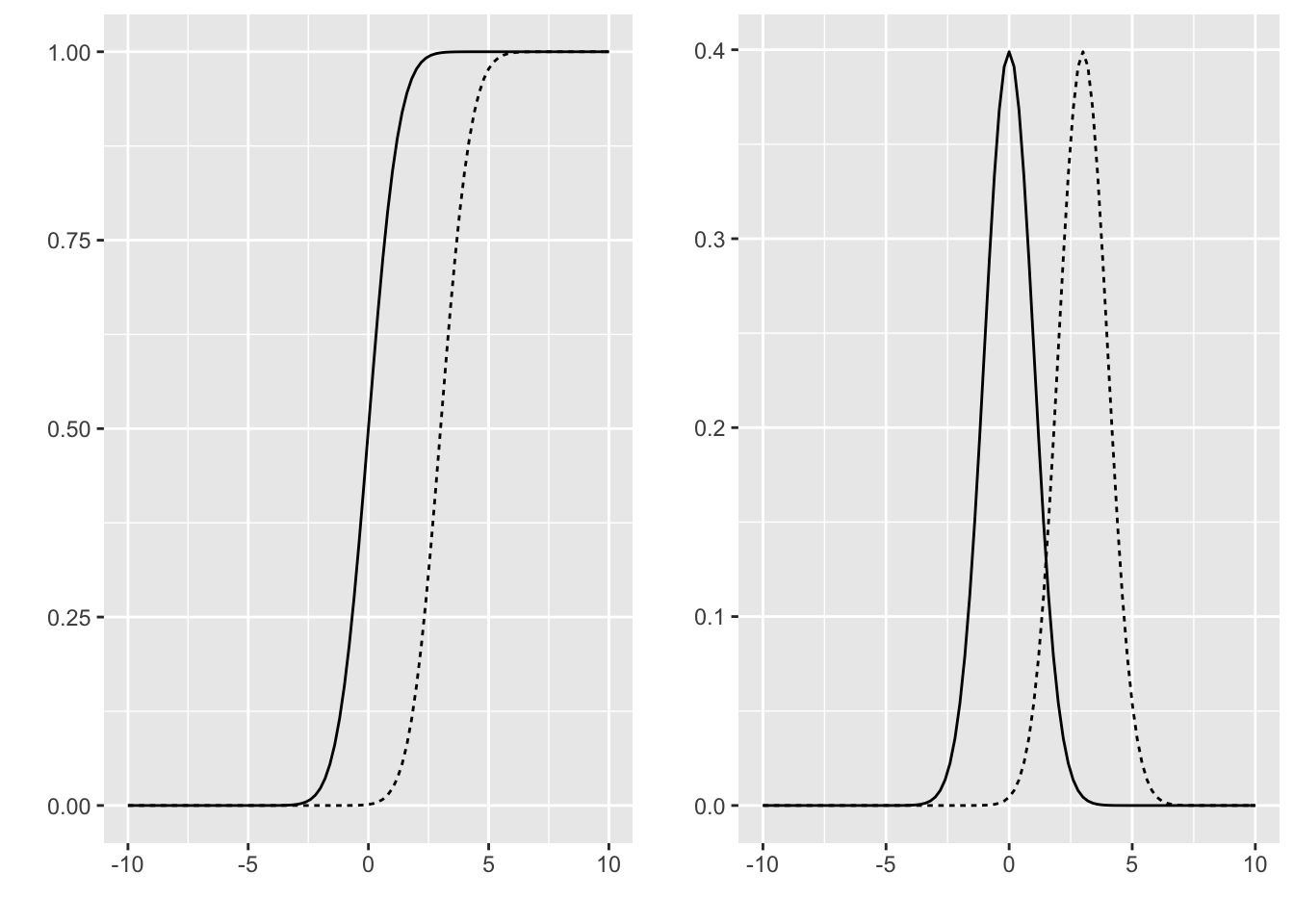
Figure 2.2: Fonction de répartition (à gauche) et densité (à droite) pour la loi N(0,1) et N(3,1)
Example 2.1 On mesure les durées de vie de 20 ampoules d’un même type. Les résultats, en heures, sont :
673, 389, 1832, 570, 522, 2694, 3683, 644, 1531, 2916.
Est-ce que l’on peut affirmer, au risque 5\(\%\), que la durée de vie d’une ampoule de ce type ne suit pas la loi exponentielle \(\mathcal E(1/1500)\) ?
On modélise donc la durée de vie de la \(i\)ème ampoule par \(X_i\), \(F\) est sa fonction de répartition inconnue et \(F_0\) est la fonction de répartition de la loi \(\mathcal E(1/1500)\).
L’idée du test de Kolmogorov est d’estimer la fonction de répartition inconnue \(F\) par la fonction de répartition empirique \(\hat F_n\) de l’échantillon \((X_1,\ldots,X_n)\) et de comparer cette fonction de répartition empirique avec la fonction de répartition donnée \(F_0\).
Definition 2.3 Pour tester \(\mathcal{H}_0\) contre \(\mathcal{H}_1\), le test de Kolmogorov est fondé sur la statistique de test \[D_n=\sup_{t \in \mathbb{R}} | \hat F_n(t)-F_0(t)|.\] La région de rejet au niveau \(\alpha\) est alors de la forme \(\mathcal{R}_{\alpha}=\{D_n \geq d_{n,1-\alpha}\}\).
Proposition 2.3 Propriétés de la statistique \(D_n\)
- La loi de \(D_n\) sous l’hypothèse \(H_0\) (\(F=F_0\)) est indépendante de \(F_0\).
- Comme \(\hat F_n\) est une fonction en escalier et que \(F_0\) est croissante, l’écart maximal entre \(\hat F_n\) et \(F_0\) est atteint en l’un des sauts de \(\hat F_n\). Ainsi, avec \(X_{(1)}\leq \ldots \leq X_{(n)}\) l’échantillon ordonné, \(X_{(0)}=-\infty\) et \(X_{(n+1)}=+\infty\), on obtient que \[ D_n=\max_{i=0,\ldots, n}\left\{\max \left( \left|\frac{i}{n}-F_0(X_{(i)})\right|; \left|\frac{i}{n}-F_0(X_{(i+1)})\right| \right)\right\}, \] ce qui permet de calculer facilement \(D_n\).
Remark. La loi de \(D_n\) sous \(H_0\) est tabulée. On trouve dans les tables les quantiles \(d_{n,1-\alpha}\) tels que \[\mathbb{P}_{H_0} (D_n \geq d_{n,1-\alpha})\leq \alpha,\] (en étant le plus proche possible de \(\alpha\)). Ces tables sont obtenues à partir de simulations de \(D_n\), sous l’hypothèse que les \(X_i\) sont i.i.d. de loi uniforme sur \([0,1]\) (\(F_0=\mathbb{1}_{[0,1]}\)). Si la loi de \(D_n\) dépendait de \(F_0\), il faudrait construire une table pour chaque loi \(F_0\).
Proposition 2.4 De la même façon, pour tester
- \(\mathcal{H}_0 : F=F_0\) contre \(\mathcal{H}^{+} : F \geq F_0\), on utilise \[D_n^{+}= \sup_{t \in \mathbb{R}} (\hat{F}_n(t)-F_0(t))\] et la région de rejet de niveau \(\alpha\) est de la forme \(\mathcal R_\alpha = \{D_n^{+} > d_{n,1-\alpha}^{+}\}\).
- \(\mathcal{H}_0 : F=F_0\) contre \(\mathcal{H}^{-} : F \leq F_0\), on utilise \[D_n^{-}= \sup_{t \in \mathbb{R}} (F_0(t) - \hat{F}_n(t))\] et la région de rejet de niveau \(\alpha\) est de la forme \(\mathcal R_\alpha = \{D_n^{-} > d_{n,1-\alpha}^{-}\}\).
Proposition 2.5 (admise) \[ \begin{array}{l l } \forall \lambda >0, \ \mathbb{P}_{\mathcal{H}_0}(\sqrt{n} D_n^+ \geq \lambda) \underset{n \rightarrow +\infty}{\longrightarrow} \exp(-2\lambda^2) & \mbox{ Smirnov (1942)} \\ \forall \lambda >0, \mathbb{P}_{\mathcal{H}_0}(\sqrt{n} D_n \geq \lambda) \underset{n \rightarrow +\infty}{\longrightarrow} 2 \sum_{k=1}^{\infty}(-1)^{k+1}\exp(-2k^2 \lambda^2) & \mbox{ Kolmogorov (1933)} \\ \forall \lambda >0, \ \mathbb{P}_{\mathcal{H}_0}(\sqrt{n} D_n \geq \lambda)\leq 2 \exp(-2\lambda^2) & \mbox{ Massart (1990) } \end{array} \]
ks.test. La p-valeur valant \(0.597\), on ne rejette pas l’hypothèse nulle au niveau \(5\%\).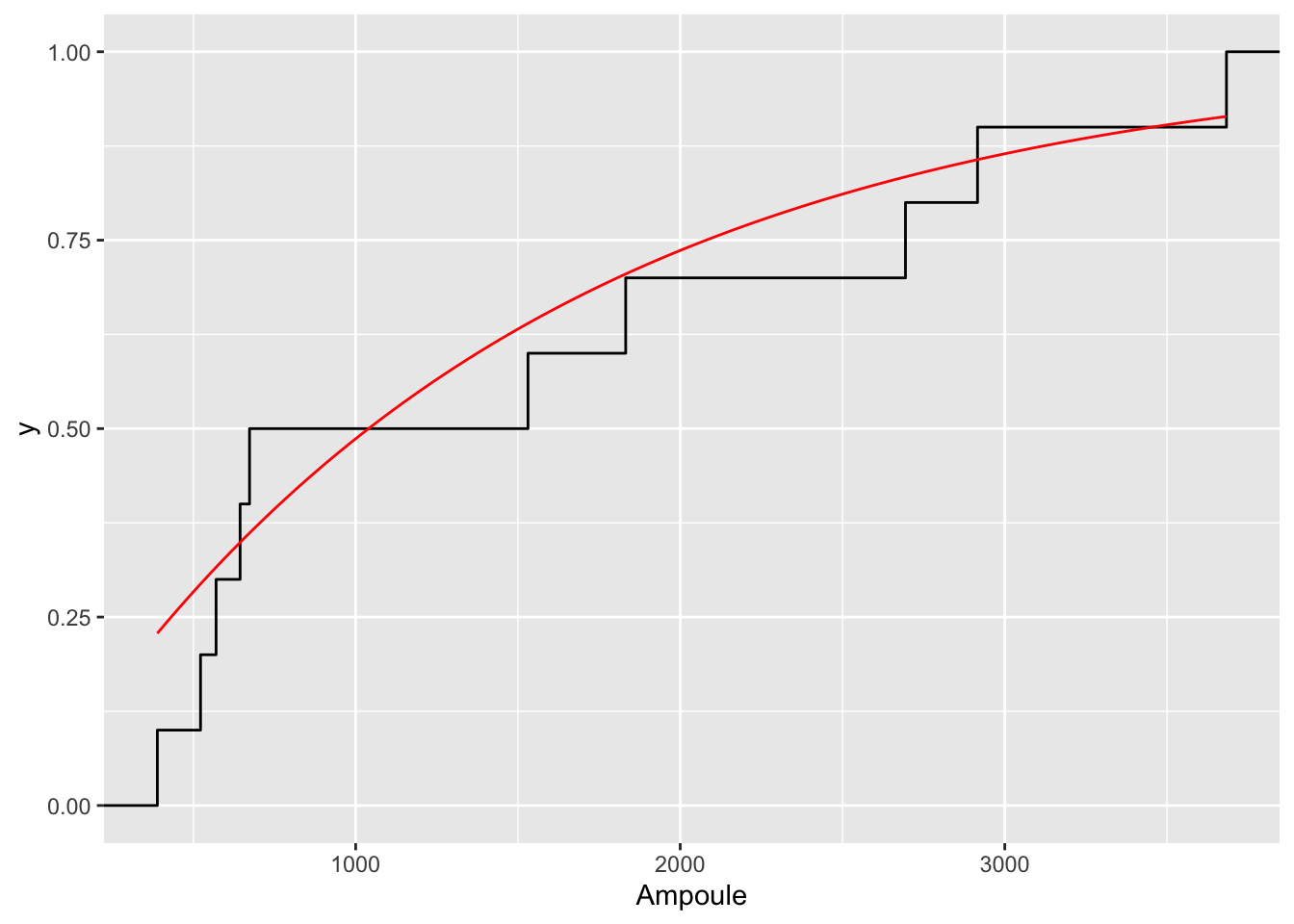
Figure 2.3: Fonction de répartition empirique et fonction de répartition de la loi E(1/1500) pour l’exemple de la durée de vie des ampoules.
Ampoule = c(673, 389, 1832, 570, 522, 2694, 3683, 644, 1531, 2916)
ks.test(Ampoule,pexp,1/1500,alternative="two.sided")
One-sample Kolmogorov-Smirnov test
data: Ampoule
D = 0.22843, p-value = 0.597
alternative hypothesis: two-sided2.3 Tests de comparaison de deux échantillons
On considère deux échantillons indépendants
- \(X_1,\ldots, X_n\) i.i.d. de fonction de répartition \(F\)
- \(Y_1, \ldots, Y_m\) i.i.d. de fonction de répartition \(G\).
On note \(N=n+m\).
Dans le cas de deux échantillons gaussiens (\(F\) correspond à une loi normale \(\mathcal{N}(m_0, \sigma^2)\) et \(G\) à la loi \(\mathcal{N}(m_1, \sigma^2)\)), on peut utiliser un test de Student pour tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \neq G\). Nous nous plaçons ici dans un cadre non paramétrique, les lois des variables \(X_i\) et \(Y_j\) ne sont pas supposées connues.
2.3.1 Tests de Kolmogorov-Smirnov
Dans cette section, on souhaite tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \neq G\). On note \(\hat F_n\) la fonction de répartition empirique de l’échantillon \((X_1, \ldots, X_n)\) et \(\hat G_m\) celle de l’échantillon \((Y_1, \ldots, Y_m)\).
Definition 2.4 Le test de Kolmogorov-Smirnov est défini par la statistique de test \[ D_{n,m}=\sup_{t \in \mathbb{R}} | \hat F_n(t)- \hat G_m(t)|. \] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_{\alpha} = \{ D_{n,m} \geq d_{n,m,1-\alpha} \}\).
Proposition 2.6 Si \(F\) est continue, la loi de \(D_{n,m}\) sous l’hypothèse nulle \(F=G\) est indépendante de \(F\). Cette loi est tabulée.
Remark. Pour faire un test unilatéral (\(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \geq G\)), on utilise la statistique de test \[ D_{n,m}^+=\sup_{t \in \mathbb{R}} (\hat F_n(t)- \hat G_m(t)). \] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_{\alpha} = \{ D^+_{n,m} \geq d^+_{n,m,1-\alpha} \}\).
Example 2.3 On souhaite comparer deux médicaments pour soulager la douleur post-opératoire. On a observé 16 patients, dont 8 ont pris le médicament A habituel, et les 8 autres un médicament B expérimental. Dans le tableau suivant sont reportés les temps (en heures) entre la prise du médicament et la sensation de soulagement.
| médicament A | médicament B |
|---|---|
| 6.8 | 4.4 |
| 3.1 | 2.5 |
| 5.8 | 2.8 |
| 4.5 | 2.1 |
| 3.3 | 6.6 |
| 4.7 | 1.5 |
| 4.2 | 4.8 |
| 4.9 | 2.3 |
Les fonctions de répartition empiriques des deux échantillons sont représentées en Figure 2.4.
Si on veut tester une différence d’efficacité entre les deux médicaments \[\mathcal{H}_0: F_A = F_B \textrm{ contre }\mathcal{H}_1: F_B\neq F_A\]
mA = c(6.8,3.1,5.8,4.5,3.3,4.7,4.2,4.9)
mB = c(4.4,2.5,2.8,2.1,6.6,1.5,4.8,2.3)
ks.test(mB, mA, alternative="two.sided")
Two-sample Kolmogorov-Smirnov test
data: mB and mA
D = 0.625, p-value = 0.08702
alternative hypothesis: two-sidedSi on veut tester si le médicament \(B\) est plus efficace que le médicament \(A\) : \[\mathcal{H}_0: F_A = F_B \textrm{ contre }\mathcal{H}_1: F_B\geq F_A\]
Two-sample Kolmogorov-Smirnov test
data: mB and mA
D^+ = 0.625, p-value = 0.04394
alternative hypothesis: the CDF of x lies above that of y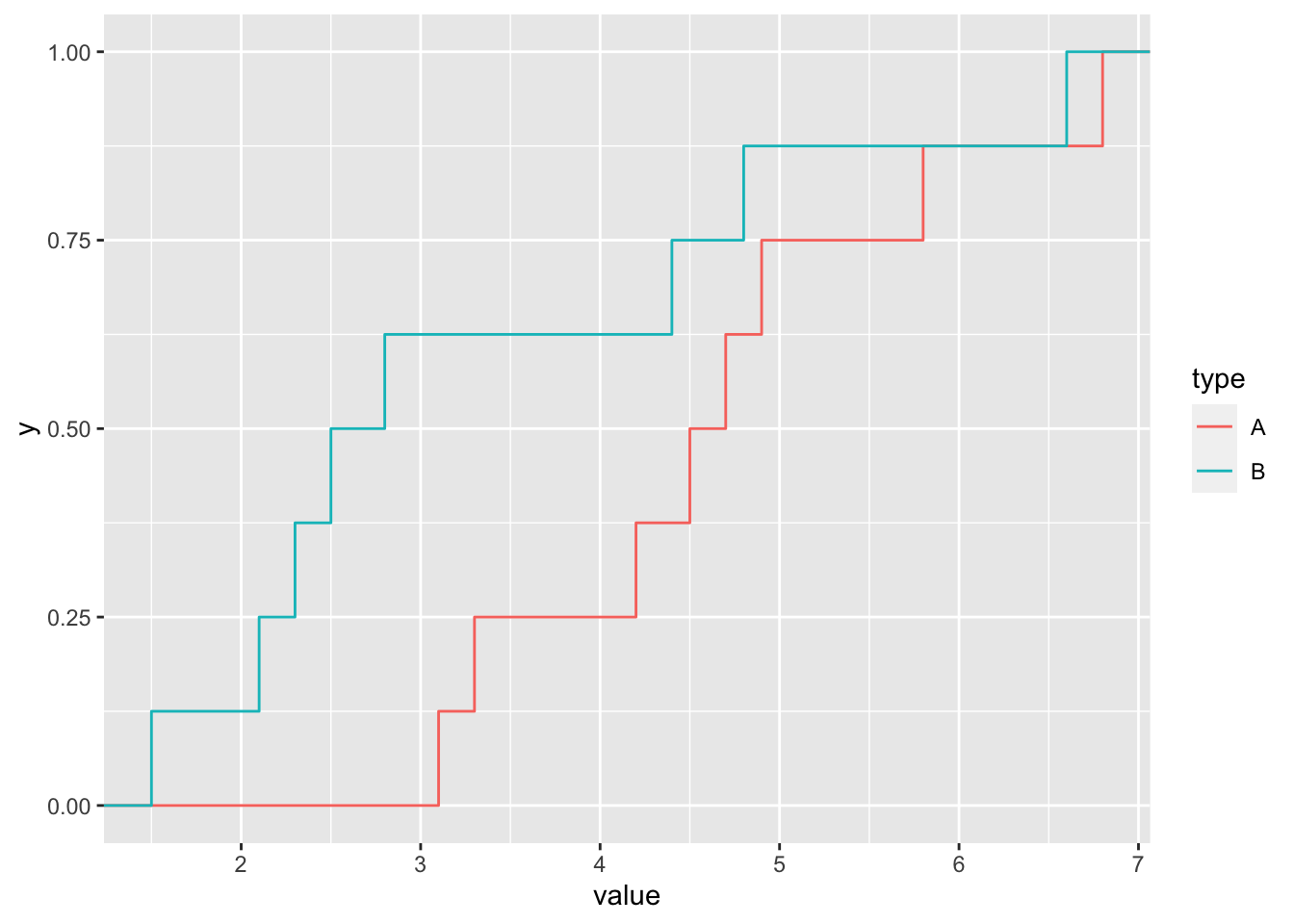
Figure 2.4: Fonction de répartition empirique pour le médicament A en rouge et le médicament B en bleu.
2.3.2 Test de Wilcoxon- Mann-Whitney
On va s’intéresser dans cette section au test de Mann-Whitney et celui de Wilcoxon (qui sont en fait équivalents) basés sur les rangs. Pour simplifier la présentation, nous allons supposer dans un premier temps qu’il n’y a pas d’ex-aequo dans les deux échantillons :
- les \(X_i\) sont tous distincts
- les \(Y_j\) sont tous distincts
- les \(X_i\) sont distincts des \(Y_j\) (\(\forall i\neq j, X_i\neq Y_j\)).
On reviendra sur le cas des ex-aequo en section 2.3.2.3.
2.3.2.1 Test de Mann-Whitney
Supposons que l’on souhaite tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \geq G\). On suppose que \(F\) et \(G\) sont continues.
Le principe du test de Mann-Whitney consiste à déterminer le nombre de couples \((X_i, Y_j)\) pour lesquels \(Y_j > X_i\). Sous \(\mathcal{H}_1\), pour tout \(t\), \(\mathbb{P}(Y\leq t) \leq P(X\leq t)\) (avec parfois l’inégalité stricte), par conséquent pour tout \(t\), \(\mathbb{P}(Y> t) \geq P(X > t)\) et le nombre de couples \((X_i, Y_j)\) pour lesquels \(Y_j > X_i\) prend des valeurs plus grandes sous \(\mathcal{H}_1\) que sous \(\mathcal{H}_0\).
Proposition 2.7 On appelle test de Mann-Whitney pour \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \geq G\) le test défini à partir de la statistique \[ MW_{X<Y} = \sum_{i=1}^n \sum_{j=1}^m \mathbb{1}_{X_i <Y_j}. \] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_{\alpha} = \{MW_{X<Y}\geq u_{(n,m),1-\alpha} \}\).
Remark. La loi de \(MW_{X<Y}\) sous \(\mathcal{H}_0\) peut être établie par récurrence (cf Caperaa and Cutsem (1988), p 126). On note \[p_{n,m}(k)=\mathbb{P}_{\mathcal{H}_0}( MW_{X<Y} =k) \mbox{ pour } k=0,1, \ldots, mn\] \[p_{n,0}(k)=p_{0,m}(k)=1 \mbox{ pour } k=0; =0 \mbox{ pour } k\neq 0.\] Alors pour tout \(k\), \[ (n+m)p_{n,m}(k)=n p_{n-1,m}(k)+ m p_{n,m-1}(k-n).\] Cette formule de récurrence permet de calculer la loi de \(MW_{X<Y}\) sous \(\mathcal{H}_0\).
On peut aussi utiliser un résultat asymptotique.
Theorem 2.1 ((Hajek (1968)) (admis)) Sous \(\mathcal{H}_0\), \[\frac{MW_{X<Y} -\mathbb{E}_{\mathcal{H}_0}[MW_{X<Y}]}{\sqrt{\mbox{Var}_{\mathcal{H}_0}(MW_{X<Y})}} \stackrel{\mathcal L}{\longrightarrow} \mathcal{N}(0,1) \mbox{ quand } n\rightarrow +\infty, n/(n+m) \rightarrow \lambda \in ]0,1[.\]
On utilise ce résultat en pratique si \(n, m \geq 8\). On a, sous l’hypothèse nulle \(\mathcal{H}_0\) que \[\mathbb{E}_{\mathcal{H}_0}[MW_{X <Y}]= \frac{mn}{2} \textrm{ et } \mbox{Var}_{\mathcal{H}_0}(MW_{X < Y})= mn \left(\frac{n+m+1}{12}\right).\]
On peut faire le raisonnement similaire pour tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \leq G\). Dans ce cas le nombre de couples \((X_i, Y_j)\) pour lesquels \(Y_j < X_i\) prend des valeurs plus grandes sous \(\mathcal{H}_1\) que sous \(\mathcal{H}_0\).
Proposition 2.8 On appelle test de Mann-Whitney pour \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \leq G\) le test défini à partir de la statistique \[ MW_{X>Y} = \sum_{i=1}^n \sum_{j=1}^m \mathbb{1}_{X_i >Y_j}. \] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_{\alpha} = \{MW_{X>Y}\geq \tilde u_{(n,m),1-\alpha} \}\).
La statistique \(MW_{X>Y}\) vérifie des propriétés similaires à celles de \(MW_{X<Y}\) vues précédemment.
Enfin dans le cas d’un test bilatéral de \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \neq G\), on combine les deux tests précédents :
Proposition 2.9 On appelle test de Mann-Whitney pour \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \neq G\) le test défini à partir de la statistique \[ MW_{X,Y} = max(MW_{X<Y},MW_{X>Y}). \] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_{\alpha} = \{MW_{X,Y}\geq v_{(n,m),1-\alpha} \}\).
2.3.2.2 Test de Wilcoxon
Revenons au test de \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \geq G\). Il existe une autre forme équivalente du test de Mann-Whitney, appelée test de la somme des rangs de Wilcoxon.
Soit \(Z = (Z_1, \ldots, Z_n,Z_{n+1}, \ldots, Z_N)=(X_1, \ldots,X_n,Y_1,\ldots, Y_m)\) l’échantillon complet. On définit \((R_1,\ldots,R_m)\) où \(R_j\) est le rang de \(Y_j\) dans l’échantillon complet ordonné \(Z_{(.)}\) : \[ R_j=\sum_{k=1}^N \mathbb{1}_{Z_k < Y_j}+1.\]
Proposition 2.10 La statistique de Wilcoxon consiste à calculer la somme des rangs des individus du deuxième échantillon : \[W_{Y}=\sum_{j=1}^m R_j.\] Comme on a la relation \[MW_{X<Y}= W_{Y} - \frac{m(m+1)}{2},\] les deux statistiques conduisent au même test.
De façon similaire, on peut construire la statistique de test de Wilcoxon \(W_{X}\) (somme des rangs des \(X_i\) dans \(Z\)) liée à la statistique de test \(MW_{X>Y}\) pour tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \leq G\).
On peut remarquer que \[ W_X + W_Y = \sum_{k=1}^{n+m} k = \frac{N (N+1)}{2}. \]
Example 2.4 On reprend l’exemple des médicaments. On veut tester si le médicament \(B\) est plus efficace que le \(A\) (\(\mathcal{H}_0: F_A=F_B\) contre \(\mathcal{H}_1: F_B \geq F_A\)). On a alors l’échantillon complet ordonné observé
\[\begin{eqnarray*} z_{(.)} &=& (1.5, 2.1, 2.3, 2.5, 2.8, 3.1, 3.3, 4.2, 4.4, 4.5, 4.7, 4.8, 4.9, 5.8, 6.6, 6.8)\\ & = & {\scriptsize (mB_6, mB_4, mB_8, mB_2, mB_3, mA_2,mA_5,mA_7,mB_1,mA_4,mA_6,mB_7,mA_8,mA_3,mB_5,mA_1)} \end{eqnarray*}\]
Les rangs observés pour les valeurs de B valent donc \[R_1=9,R_2=4,R_3=5,R_4=2,R_5=15,R_6=1, R_7=12, R_8=3\] ce qui donne \(W_B=51\) et \(W_A=(16\times 17)/2 - 51 = 85\).
On a également que \[\begin{eqnarray*} MW_{B<A}&=&\sum_{i=1}^8\sum_{j=1}^8 \mathbb{1}_{B_i < A_j}\\ &=& 5+ 5+5+6+6+7+7+8 = 49 = W_A - (8 \times 9) /2 \end{eqnarray*}\]
et
\[\begin{eqnarray*} MW_{B>A} &=& \sum_{i=1}^8\sum_{j=1}^8 \mathbb{1}_{B_i > A_j} \\ &=& 3+3+3+2+2+1+1+0=15 = W_B - (8 \times 9) /2. \end{eqnarray*}\]
Wilcoxon rank sum exact test
data: mB and mA
W = 15, p-value = 0.04149
alternative hypothesis: true location shift is less than 02.3.2.3 Traitement des ex-aequos
Nous avons supposé les lois continues, donc la probabilité d’avoir des ex-aequos est nulle. En pratique, soit parce que les lois ne sont pas continues, soit parce qu’on a des mesures arrondies, on peut avoir des ex-aequos. Dans ce cas, on peut considérer les statistiques de test de Mann-Whitney suivantes : \[ \tilde{MW}_{X<Y} = \sum_{i=1}^n \sum_{j=1}^m \left\{\mathbb{1}_{X_i <Y_j} + \frac 1 2 \mathbb{1}_{X_i =Y_j} \right\} \] et \[ \tilde{MW}_{X>Y} = \sum_{i=1}^n \sum_{j=1}^m \left\{\mathbb{1}_{X_i >Y_j} + \frac 1 2 \mathbb{1}_{X_i =Y_j} \right\} \] respectivement. On peut remarquer que \(\tilde{MW}_{X<Y} +\tilde{MW}_{X>Y} =nm\).
Pour le test de Wilcoxon, on utilise les rangs moyens : le rang de tous les éléments d’un groupe d’ex-aequos est la moyenne des rangs des éléments du groupe. On corrige ainsi les \(R_j\) définis précédemment.
Example 2.5 On considère les valeurs observées suivantes pour les deux échantillons : \[ \underline{x} = (5,3,6,8,1,6) \textrm { avec } n=6 \textrm{ et } \underline{y} = (5,7,9,5,2) \textrm { avec } m=5. \] On obtient alors le tableau des valeurs ordonnées et rangs suivant :
| \(x_{(.)}\) | 1 | 3 | 5 | 6 | 6 | 8 | |||||
| \(y_{(.)}\) | 2 | 5 | 5 | 7 | 9 | ||||||
| \(\tilde R_i\) | 1 | 3 | 5 | 7.5 | 7.5 | 10 | |||||
| \(\tilde R_j\) | 2 | 5 | 5 | 9 | 11 |
Ainsi \[\left(\tilde MW_{X<Y} \right)^{obs} = 1 + (2+\frac 1 2) + (2+\frac 1 2) +5+6=17,\] \[\left(\tilde W_Y\right)^{obs} = \sum_{j=1}^{5} \tilde R_j = 2+5+5+9+11=32\] et on retrouve bien que \(\left(\tilde MW_{X<Y} \right)^{obs} =\tilde W_Y^{obs} - \frac{5\times 6}{2}.\)
2.3.3 Test de la médiane
On veut tester \(\mathcal{H}_0\): \(F=G\) contre \(\mathcal{H}_1\): \(F \geq G\) et on suppose que \(F\) et \(G\) sont continues. Le principe du test de la médiane consiste à déterminer le nombre de variables du deuxième échantillon qui sont supérieures à la médiane de l’ensemble des observations.
Definition 2.5 Le test de la médiane est défini à partir de la statistique \[ M_{X,Y}= \frac1m \sum_{j=1}^m \mathbb{1}_{R_j >\frac{N+1}{2}}.\] La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_\alpha = \{M_{X,Y} \geq m_{n,m,1-\alpha}\}\).
Example 2.6 Test de localisation.
\(X_1, \ldots, X_n\) sont i.i.d. de fonction de répartition \(F\) et \(Y_1, \ldots, Y_m\) sont i.i.d. de fonction de répartition \(G=F(.-\mu)\). Par exemple, on étudie la pression artérielle de patients soumis à un traitement contre l’hypertension \((Y_j)\), et on les compare à des patients non traités \((X_i)\). Supposons qu’après traitement, la loi de la pression artérielle est translatée de \(\mu\). Le traitement est efficace si \(\mu <0\), il est inefficace si \(\mu=0\).
Loi de \(M_{X,Y}\) sous \(\mathcal{H}_0\) :
- Si \(N\) pair,
\[ \forall k\in \left\{ \max(0, m - \frac N 2),\ldots,\min(m, \frac N 2)\right\}, \mathbb{P}_{\mathcal{H}_0}(m M_{X,Y}=k)=\frac{C_m^k C_{N-m}^{N/2-k}}{C_{N}^{N/2}}. \] Donc \(n M_{X,Y}\) suit une loi hypergéométrique \(\mathcal{H}(N,\frac N 2, m)\).
On en déduit que \(\mathbb{E}_{\mathcal{H}_0}[M_{X,Y}] = \frac 1 2\) et \(\mbox{Var}_{\mathcal{H}_0}(M_{X,Y}) = \frac{n}{4m(N-1)}\).
- Si \(N\) est impair,
\[ \forall k\in \left\{ \max(0,m- \frac{N+1}{ 2}),\ldots,\min(m, \frac{N-1}{ 2}) \right\}, \mathbb{P}_{\mathcal{H}_0}(m M_{X,Y}=k)=\frac{C_m^k C_{N-m}^{\frac{N-1}{2}-k}}{C_{N}^{\frac{N-1}{2}}}. \] Donc \(n M_{X,Y}\) suit une loi hypergéométrique \(\mathcal{H}(N,\frac{N-1}{2}, m)\).
On en déduit que \(\mathbb{E}_{\mathcal{H}_0}[M_{X,Y}] = \frac{N-1}{2N}\) et \(\mbox{Var}_{\mathcal{H}_0}(M_{X,Y}) = \frac{n(N+1)}{4mN^2}\).
La connaissance de la loi de \(M_{X,Y}\) sous \(\mathcal{H}_0\) permet de déterminer la région de rejet du test. Pour \(n,m \geq 30\), on peut approximer la loi de \(M_{X,Y}\) sous \(\mathcal{H}_0\) par la loi \(\mathcal{N}(\mathbb{E}_{\mathcal{H}_0}[M_{X,Y}],\mbox{Var}_{\mathcal{H}_0}(M_{X,Y}))\).
2.4 Tests de normalité
Dans cette section, on considère un \(n\)-échantillon \((X_1,\ldots,X_n)\) de fonction de répartition \(F\). On note \(\hat F_n\) la fonction de répartition empirique associée à cet échantillon.
Pour illustrer les différentes méthodes, nous allons considérer les trois échantillons de taille \(n=200\) suivants :
- Ech1 : un échantillon simulé selon la loi \(\mathcal N(2,1)\)
- Ech2 : un échantillon simulé selon la loi uniforme sur l’intervalle \([2,4]\)
- Ech3 : un échantillon simulé selon la loi de Cauchy de paramètre 1
2.4.1 Méthode graphique : droite de Henry
La méthode de la droite de Henry, aussi appelée “Normal Probability Plot’’ ou”Q-Q Plot’’, consiste à représenter les points \((X_{(i)}, \Phi^{-1}\circ \hat{F}_n(X_{(i)}))\), où \(X_{(1)} \leq \ldots \leq X_{(n)}\) est l’échantillon ordonné et \(\Phi\) représente la fonction de répartition de la loi \(\mathcal{N}(0,1)\). Notons que \(\hat F_n(X_{(i)})=i/n\). Sous l’hypothèse que les \(X_i\) sont i.i.d. de loi normale, les points \((X_{(i)}, \Phi^{-1}\circ \hat F_n(X_{(i)}))\) sont pratiquement alignés. Le Q-Q plot pour les trois échantillons simulés est donné en Figure 2.5.
![\label{QQplot} Q-Q plot pour les 3 échantillons (N(2,1) à gauche, U([2,4]) au centre, et C(1) à droite)](Bookdown-poly_files/figure-html/QQplot-1.png)
Figure 2.5: Q-Q plot pour les 3 échantillons (N(2,1) à gauche, U([2,4]) au centre, et C(1) à droite)
2.4.2 Test de normalité de Kolmogorov-Smirnov (de Lilliefors)
On souhaite tester l’hypothèse \(\mathcal{H}_0\) : “les \(X_i\) suivent une loi normale”, contre l’hypothèse \(\mathcal{H}_1\) : “les \(X_i\) ne suivent pas une loi normale”. On note
\[ \bar{X}=\frac1n \sum_{i=1}^n X_i, \ S^2=\frac1{n-1} \sum_{i=1}^n (X_i-\bar{X})^2. \]
Definition 2.6 Le test de normalité de Kolmogorov est fondé sur la statistique de test \[ D\mathcal{N}_n=\sup_{t \in \mathbb{R}}| \hat F_n(t)-\Phi(t; \bar{X},S^2)| \] où \(\Phi(. ; \bar{X},S^2)\) est la fonction de répartition de la loi normale \(\mathcal{N}(\bar{X},S^2)\). La région de rejet au niveau \(\alpha\) est de la forme \(\mathcal R_\alpha = \{ D\mathcal{N}_n > d_{n,1-\alpha}\}\).
Proposition 2.11 Sous l’hypothèse \(\mathcal{H}_0\), i.e les \(X_i\) suivent une loi normale \(\mathcal{N}(\mu, \sigma^2)\), la loi de \(D\mathcal{N}_n\) ne dépend pas des paramètres inconnus \((\mu, \sigma^2)\). Il s’agit de la loi de \[ KS\mathcal{N}_n = \underset{t\in\mathbb{R}}{\sup}\ \left| \hat{\Phi}_n(t) - \Phi\left(\frac{t - \hat\mu_{\mathcal{Z}}}{S_{\mathcal{Z}}}\right) \right| \] où \(\mathcal{Z}=(Z_1,\ldots,Z_n)\) i.i.d de loi \(\mathcal{N}(0,1)\), \(\hat\Phi_n\) la fonction de répartition empirique de \(\mathcal{Z}\), \(\hat\mu_{\mathcal{Z}}\) la moyenne empirique et \(S^2_{\mathcal{Z}}\) la variance empirique de \(\mathcal{Z}\).
La loi de \(D\mathcal{N}_n\) est tabulée (on peut par exemple la simuler avec \(\mu=0\) et \(\sigma^2=1\) pour en estimer les quantiles).
On applique le test de normalité de Kolmogorov-Smirnov sur les trois échantillons simulés :
Lilliefors (Kolmogorov-Smirnov) normality test
data: Ech1
D = 0.041892, p-value = 0.532
Lilliefors (Kolmogorov-Smirnov) normality test
data: Ech2
D = 0.083624, p-value = 0.001691
Lilliefors (Kolmogorov-Smirnov) normality test
data: Ech3
D = 0.34735, p-value < 2.2e-162.4.3 Test de Shapiro-Wilk
Il s’agit d’un test basé sur les \(L\)-statistiques (combinaison linéaire des statistiques d’ordre), qui se base sur une comparaison de la variance empirique avec un estimateur de la variance des \(X_i\) qui a de bonnes propriétés sous l’hypothèse de normalité.
2.4.3.1 Estimation de la moyenne et de la variance à l’aide des statistiques d’ordre pour des lois symétriques
Soit \(X_1, \ldots, X_n\) i.i.d. On note \(\mu=\mathbb{E}[X_i]\) et \(\sigma^2=\mbox{Var}(X_i)\). La loi de \(Y_i=(X_i-\mu)/\sigma\) est supposée symétrique (ce qui signifie que \(-Y_i\) a même loi que \(Y_i\)). On note \((X_{(1)}, \ldots, X_{(n)})\) l’échantillon des \(X_i\) ordonné : \(X_{(1)} \leq \ldots \leq X_{(n)}\). On note \((Y_{(1)}, \ldots, Y_{(n)})\) l’échantillon des \(Y_i\) ordonné. On a \[Y_{(i)}=(X_{(i)}-\mu)/\sigma.\] Pour \(i, j \in \{1, \ldots,n\}\), on note \(\alpha_i=\mathbb{E}[Y_{(i)}]\) et \(B_{i,j}=\mbox{Cov}(Y_{(i)},Y_{(j)}).\) On a alors \[X_{(i)}= \mu+\alpha_i \sigma +\varepsilon_i,\] avec \(\mathbb{E}[\varepsilon_i]=0\). Les \(\varepsilon_i\) ne sont pas indépendantes. La matrice de variance-covariance du vecteur \(\varepsilon=(\varepsilon_1, \ldots, \varepsilon_n)'\) est \(\sigma^2 B\). On note \(1_n\) et \(\alpha\) les vecteurs de \(\mathbb{R}^n\) définis par \[1_n=\left( \begin{array}{c} 1\\ 1\\ .\\ .\\ 1\end{array} \right), \quad \alpha=\left(\begin{array}{c} \alpha_1\\ \alpha_2\\ .\\ .\\ \alpha_n \end{array}\right).\] On note \(A\) la matrice de taille \((n,2)\) définie par \(A=(1_n, \alpha)\). Enfin, on note \(X_{(.)}=(X_{(1)}, \ldots, X_{(n)})'\) et \(\varepsilon=(\varepsilon_1, \ldots, \varepsilon_n)'\). On a la relation \[X_{(.)}= A \left( \begin{array}{c} \mu \\ \sigma \end{array}\right) + \varepsilon.\] L’estimateur des moindres carrés pondérés de \((\mu, \sigma)\) est obtenu en minimisant en les paramètres \((\mu, \sigma)\) le critère : \[\left( X_{(.)}- A \left( \begin{array}{c} \mu \\ \sigma \end{array}\right)\right)' B^{-1} \left( X_{(.)}- A \left(\begin{array}{c} \mu \\ \sigma\end{array}\right)\right).\] On obtient comme solution de ce système \[\left( \begin{array}{c} \hat{\mu}_n \\ \hat{\sigma}_n \end{array}\right)= (A'B^{-1} A)^{-1} A'B^{-1} X_{(.)}.\] (cf cours sur le modèle linéaire)
\[A'B^{-1} A = \left( \begin{array}{c c } 1_n'B^{-1} 1_n & 1_n'B^{-1} \alpha \\ \alpha' B^{-1} 1_n & \alpha' B^{-1} \alpha \end{array}\right).\]
Lemma 2.1 Lorsque la loi des \(Y_i\) est symétrique, \(1_n'B^{-1} \alpha =0\) , la matrice \(A'B^{-1} A\) est donc diagonale.
Il en résulte que \[\hat{\mu}_n= \frac{ 1_n'B^{-1} X_{(.)}}{ 1_n'B^{-1} 1_n},\quad \hat{\sigma}_n= \frac{ \alpha'B^{-1} X_{(.)}}{ \alpha'B^{-1} \alpha}.\] On peut montrer que, si la loi des \(Y_i\) n’est pas symétrique, \(\hat{\sigma}_n\) sous-estime \(\sigma\).
2.4.3.2 Procédure de test
Definition 2.7 Soit \(Y_1, \ldots Y_n\) i.i.d. de loi \(\mathcal{N}(0,1)\) et \(Y_{(1)} \leq \ldots \leq Y_{(n)}\) l’échantillon ordonné. Soit \(\alpha=(\mathbb{E}[Y_{(1)}], \ldots\mathbb{E}[Y_{(n)}] )'\). Soit \(B\) la matrice de covariance du vecteur \((Y_{(1)},\ldots , Y_{(n)})\). Le test de Shapiro-Wilk pour tester l’hypothèse de normalité des \(X_i\) est basé sur la statistique de test : \[ SW_n=\frac{\hat{\sigma}_n^2 (\alpha' B^{-1} \alpha)^2}{\sum_{i=1}^n (X_i-\bar{X}_n)^2 (\alpha' B^{-2} \alpha)}. \] On peut l’écrire sous la forme \[SW_n= \frac{\left(\sum_{i=1}^n a_i X_{(i)}\right)^2}{ \sum_{i=1}^n (X_i-\bar{X}_n)^2},\] avec \[(a_1, \ldots,a_n)=\frac{\alpha' B^{-1}}{(\alpha' B^{-1}B^{-1}\alpha)^{1/2}}.\] La région de rejet est de la forme \(\{SW_n \leq c_{n, \alpha}\}\).
Les \(a_i\) sont tabulés, ce qui permet de calculer facilement \(SW_n\), les quantiles \(c_{n,\alpha}\) sont également tabulés. On peut interpréter \(SW_n\) comme une mesure de corrélation (au carré) entre les données ordonnées et les statistiques d’ordre d’une loi normale.
Le test de Shapiro-Wilk est ici appliqué sur les trois échantillons simulés :
Shapiro-Wilk normality test
data: Ech1
W = 0.99268, p-value = 0.4201
Shapiro-Wilk normality test
data: Ech2
W = 0.95826, p-value = 1.289e-05
Shapiro-Wilk normality test
data: Ech3
W = 0.45775, p-value < 2.2e-16References
Caperaa, P., and B. van Cutsem. 1988. Méthodes et Modèles En Statistique Non Paramétrique : Exposé Fondamental. Dunod.