Initiation au langage et objets de R

Structure des objets

Sous R, les éléments de base sont des objets : des données (vecteurs, matrices, …), des fonctions, des graphiques, … Ces objets se différencient par leur mode décrivant leur contenu, et leur classe décrivant leur structure. Les objets atomiques sont de mode homogène et les objets récursifs sont de mode hétérogène. Les différents modes sont null (objet vide), logical, numeric, complex, character.

Les classes d’objets les plus courantes sont : vector, matrix, array, factor, data.frame, list. On peut avoir des vecteurs, matrices, tableaux, … de mode null (objet vide), logical (TRUE, FALSE, NA), numeric, complex, character. Par contre les listes et les tableaux peuvent être composés d’éléments hétérogènes. On utilise la commande class() pour connaître la classe d’un objet et str()pour connaitre la nature des éléments composant l’objet.

La principale difficulté en R réside dans l’identification des types d’objets manipulés. Nous allons dans ce tutoriel présenter ces différents objets, les opérations et manipulations basiques que l’on peut faire, …

On peut stocker un objet dans une variable (ex a) à l’aide de a<- ... ou a= .... Pour lister les variables actuellement disponibles dans la session de travail, on utilise la fonction ls(). Pour effacer une ou plusieurs variables, on utilise la fonction rm(). La commande rm(list=ls()) permet d’effacer toutes les variables en mémoire.

Opération sur les scalaires

Opérations

Les opérations élémentaires sur les scalaires sont *,-, +, /, ^.

Sous R, tapez les commandes suivantes. Vous chercherez en particulier à bien identifier les différents types de données :

2 + 2
exp(10)
a = log(2)
a
b = cos(10)
b
a - b
a * b
d <- 2 < 3
d
dd <- FALSE
dd - d
dd + d
e <- "toto"
class(e)
str(e)

`is.xxx()/as.xxx()`

Pour tester si un objet obj est de type xxx, on utilise la commande is.xxx(obj). On peut aussi contraindre si possible l’objet obj au type xxx avec la commande as.xxx(obj).

a = 4.3
is.numeric(a)

[1] TRUE

is.complex(a)

[1] FALSE

is.character(a)

[1] FALSE

as.character(a)

[1] "4.3"

b <- "toto"
is.numeric(b)

[1] FALSE

as.list(b)

[[1]]
[1] "toto"

Arrondir

Pour obtenir des valeurs arrondies sur des valeurs numériques, vous pouvez utiliser l’une des commandes suivantes round(), ceiling(), floor(), trunc() ou signif() (voir l’aide ?round). Comparez les codes suivantes:

a = 1.3579
floor(a)

[1] 1

ceiling(a)

[1] 2

round(a, digits = 2)

[1] 1.36

signif(a, digits = 2)

[1] 1.4

is.integer(floor(a))

[1] FALSE

is.numeric(floor(a))

[1] TRUE

Booléens et opérations logiques

En R, un booléen est représenté par TRUE ou FALSE. Les opérations logiques, <, >, <=, >=, != (différent), == (égal) retournent TRUE ou FALSE. On peut définir plusieurs conditions à remplir avec les opérateurs & (ET) et | (OU).

Attention, R considère qu’un booléen a FALSE vaut $0$ et qu’un booléen a TRUE vaut $1$. Il est donc capable d’évaluer TRUE + 5 bien qu’en toute logique, cela n’a aucun sens!

Voici quelques exemples de manipulation des booléens :

a = 3
b = 6
a <= b

[1] TRUE

a != b

[1] TRUE

(b - 3 == a) & (b >= a)

[1] TRUE

(b == a) | (b >= a)

[1] TRUE

Les caractères

On donne ici quelques fonctions de base sur la manipulation des chaînes de caractères. Dans le tutoriel 4 de R avancé, on présentera le package stringr qui est très utilisé pour gérer et manipuler des chaînes de caractères.

`paste()`

Pour concaténer, juxtaposer des chaînes de caractères on utilise la fonction paste()

Ex = paste("Bonjour", "à", "toutes", "et", "tous", "!")
paste("Bonjour", "à", "toutes", "et", "tous", "!", sep = "_")

[1] "Bonjour_à_toutes_et_tous_!"

x = c("Bonjour", "à", "vous")
paste(x)

[1] "Bonjour" "à"       "vous"

paste(x, collapse = "++")

[1] "Bonjour++à++vous"

`nchar()`

On accède à la longueur d’une chaîne avec la fonction nchar()

nchar(Ex)

[1] 26

`substr()` / `substring()`

La fonction substr() permet d’extraire une partie d’une chaîne à partir des attributs « start » et « stop ». On peut aussi remplacer des segments d’une chaine.

substr(Ex, start = 3, stop = 9)

[1] "njour à"

substr(Ex, start = 3, stop = 9) <- "@@@"
Ex

[1] "Bo@@@ur à toutes et tous !"

On peut aussi utiliser la fonction substring()

Ex = paste("Bonjour", "à", "toutes", "et", "tous", "!")
substring(Ex, first = 3)

[1] "njour à toutes et tous !"

substring(Ex, first = 3, last = 9) <- "@@@--<"
Ex

[1] "Bo@@@--<à toutes et tous !"

`strsplit()`

La fonction strsplit() permet de scinder une chaîne de caractères :

Ex = paste("Bonjour", "à", "toutes", "et", "tous", "!")
strsplit(Ex, split = " ")

[[1]]
[1] "Bonjour" "à"       "toutes"  "et"      "tous"    "!"

strsplit(Ex, split = c("o", " "))

[[1]]
[1] "B"         "nj"        "ur à t"    "utes et t" "us !"

La sortie de la fonction strsplit() est une liste (voir section sur list)

`grep()`

La fonction grep() permet de rechercher les éléments d’une liste.

Ex1 = c("tomate", "concombre", "mais", "courgette", "poivron", "carotte", "betterave")
Ex1

[1] "tomate"    "concombre" "mais"      "courgette" "poivron"   "carotte"  
[7] "betterave"

grep(pattern = "o", Ex1, value = FALSE)  # donne les indices des éléments contenant un 'o' dans Ex

[1] 1 2 4 5 6

grep(pattern = "o", Ex1, value = TRUE)  # Donne les éléments de Ex1 qui contiennent la lettre 'o'

[1] "tomate"    "concombre" "courgette" "poivron"   "carotte"

On peut utiliser la fonction grep() avec les expressions régulières disponible sous R, il faut penser à mettre l’option fixed=FALSE. Pour plus de détail, voir ?regex.

`gsub()`

Enfin pour remplacer un pattern dans une chaine de caractère, on peut utiliser la fonction gsub()

gsub(pattern = "o", replacement = "@", Ex1, fixed = TRUE)

[1] "t@mate"    "c@nc@mbre" "mais"      "c@urgette" "p@ivr@n"   "car@tte"  
[7] "betterave"

Vecteurs (vector)

Un vecteur est un ensemble ordonné d’éléments de même nature (numérique, logique ou alphanumérique). La création d’un vecteur peut se faire par la commande c(e1,e2,...). On peut également générer une séquence avec la commande seq(a,b,t) où $a$ est le premier terme, le dernier terme est $\leq b$ et le pas est $t$. Pour créer un vecteur constitué de l’élément $x$ répété $n$ fois, on utilise la commande rep(x,n).

Exemples

On donne ici quelques exemples à tester sous R pour vous familiariser avec les vecteurs. En particulier, vous pouvez découvrir des fonctions utiles avec les vecteurs comme length(), sum(), sort(), … , les opérations usuelles, l’extraction d’éléments d’un vecteur, …

Commande `c(...)`

d <- c(2, 3, 5, 8, 4, 6)
d

[1] 2 3 5 8 4 6

is.vector(d)

[1] TRUE

c(2, 5, "toto")

[1] "2"    "5"    "toto"

1:10

 [1]  1  2  3  4  5  6  7  8  9 10

Commande `seq(...)`

seq(1, 10)

 [1]  1  2  3  4  5  6  7  8  9 10

seq(from = 1, to = 20, by = 2)

 [1]  1  3  5  7  9 11 13 15 17 19

seq(1, 20, by = 5)

[1]  1  6 11 16

seq(1, 20, length = 5)

[1]  1.00  5.75 10.50 15.25 20.00

Commande `rep(...)`

rep(5, times = 10)

 [1] 5 5 5 5 5 5 5 5 5 5

rep(c(1, 2), 3)

[1] 1 2 1 2 1 2

rep(c(1, 2), each = 3)

[1] 1 1 1 2 2 2

Extraire des éléments

[1] 2 3 5 8 4 6

d[2]

[1] 3

d[2:3]

[1] 3 5

d[c(1, 3, 6)]

[1] 2 5 6

d[-3]

[1] 2 3 8 4 6

d[-(1:2)]

[1] 5 8 4 6

Opérations

Additionner ou soustraire un scalaire d’un vecteur

d + 4

[1]  6  7  9 12  8 10

d - 4

[1] -2 -1  1  4  0  2

Multiplier ou diviser un vecteur par un scalaire

2 * d

[1]  4  6 10 16  8 12

d/3

[1] 0.6666667 1.0000000 1.6666667 2.6666667 1.3333333 2.0000000

Multiplier/ diviser deux vecteurs terme à terme

e <- rep(2, 6)
d * e

[1]  4  6 10 16  8 12

d/e

[1] 1.0 1.5 2.5 4.0 2.0 3.0

Fonctions usuelles

d = c(2, 3, 5, 8, 4, 6)
d

[1] 2 3 5 8 4 6

Longueur d’un vecteur

length(d)

[1] 6

Somme des termes d’un vecteur numérique

sum(d)

[1] 28

Somme des termes cumulés d’un vecteur numérique

cumsum(d)

[1]  2  5 10 18 22 28

Différence des termes successifs d’un vecteur numérique

diff(d)

[1]  1  2  3 -4  2

Vérifier si d est un vecteur

is.vector(d)

[1] TRUE

Transposition d’un vecteur

t(d)

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    2    3    5    8    4    6

Produit scalaire

t(d) %*% e

     [,1]
[1,]   56

NA (Not Available) signale une donnée manquante

d[3] <- NA
d

[1]  2  3 NA  8  4  6

is.na(d)

[1] FALSE FALSE  TRUE FALSE FALSE FALSE

any(is.na(d))

[1] TRUE

all(is.na(d))

[1] FALSE

Autres fonctions intéressantes avec les vecteurs : abs(), sort(), order(), which(), …

a <- c(3, -1, 5, 2, -7, 3, 9)
abs(a)

[1] 3 1 5 2 7 3 9

sort(a)

[1] -7 -1  2  3  3  5  9

order(a)

[1] 5 2 4 1 6 3 7

b = a == 3
b

[1]  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE

sort(b)

[1] FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE

text <- c("petit", "moyen", "grand")
is.vector(text)

[1] TRUE

f = c(a = 12, b = 26, c = 32, d = 41)
f

 a  b  c  d 
12 26 32 41

names(f)

[1] "a" "b" "c" "d"

f["a"]

 a 
12

names(f) <- c("a1", "a2", "a3", "a4")
f

a1 a2 a3 a4 
12 26 32 41

Notez la différence entre les commandes suivantes :

f > 30

   a1    a2    a3    a4 
FALSE FALSE  TRUE  TRUE

f[f > 30]

a3 a4 
32 41

which(f > 30)

a3 a4 
 3  4

f[2] <- 22
f + 100

 a1  a2  a3  a4 
112 122 132 141

Etonnant ces commandes suivantes, non ?

a1 a2 a3 a4 
12 22 32 41

[1]  2  3 NA  8  4  6

f + d

[1] 14 25 NA 49 16 28

On peut appliquer une fonction à tous les éléments d’un vecteur facilement.

cos(f)

        a1         a2         a3         a4 
 0.8438540 -0.9999608  0.8342234 -0.9873393

Exercice

Enoncé

Question 1 : Créer les vecteurs suivants :

le vecteur $a$ constitué des entiers pairs jusqu’à 30
le vecteur $b$ contenant $v=5$, deux fois la valeur de $v$, puis un tiers de la valeur de $v$, puis trois fois $v^2$, puis $\sqrt{v}$, puis le quatrième élément de $a$.
le vecteur $c$ contenant 6 chiffres compris entre 4 et 30 avec un intervalle constant.
le vecteur $d$ contenant la somme des éléments de $c$, puis la longueur de $b$, puis 5 fois le chiffre 3.

Question 2 : Extraire du vecteur $a$ :

le quatrième élément
tous les éléments sauf le quatrième
tous les éléments supérieurs à 10

Question 3 : À quoi sert la fonction unique ? Illustrer son fonctionnement sur un exemple.

Correction

Question 1 :

a = seq(2, 30, 2)
a

 [1]  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30

v = 5
b = c(v, 2 * v, v/3, 3 * (v^2), sqrt(v), a[4])
b

[1]  5.000000 10.000000  1.666667 75.000000  2.236068  8.000000

c = seq(4, 30, length = 6)
c

[1]  4.0  9.2 14.4 19.6 24.8 30.0

d = c(sum(c), length(b), rep(3, 5))
d

[1] 102   6   3   3   3   3   3

Question 2 :

a[4]

[1] 8

a[-4]

 [1]  2  4  6 10 12 14 16 18 20 22 24 26 28 30

a[a > 10]

 [1] 12 14 16 18 20 22 24 26 28 30

Question 3 :

help(unique)
unique(d)

[1] 102   6   3

La fonction unique() permet de récupérer les éléments d’un vecteur (et pas que) sans réplication.

Matrices (matrix)

Comme les vecteurs, les matrices sont de mode quelconque mais ne contiennent que des éléments de même nature. Pour créer une matrice, on utilise la commande matrix(vec,nrow=n,ncol=p) où vec est le vecteur contenant les éléments de la matrice de taille $n$ par $p$, qui seront rangés en colonne sauf si l’option byrow=T est utilisée.

Exemples

On donne ici quelques exemples à tester sous R pour vous familiariser avec les matrices. En particulier, vous pouvez découvrir des fonctions utiles avec les matrices comme dim(), t(), cbind(), rbind()… , les opérations usuelles dont la différence entre A*B et A%*%B, l’extraction d’éléments d’une matrice, …

`matrix()`

A = matrix(1:15, ncol = 5)
A

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

class(A)

[1] "matrix" "array"

B = matrix(1:15, nc = 5, byrow = T)
B2 = B
B2[1, 1] = "toto"
B2

     [,1]   [,2] [,3] [,4] [,5]
[1,] "toto" "2"  "3"  "4"  "5" 
[2,] "6"    "7"  "8"  "9"  "10"
[3,] "11"   "12" "13" "14" "15"

rownames(A) = c(paste("ligne", 1:3, sep = ""))
A

       [,1] [,2] [,3] [,4] [,5]
ligne1    1    4    7   10   13
ligne2    2    5    8   11   14
ligne3    3    6    9   12   15

Extraire

       [,1] [,2] [,3] [,4] [,5]
ligne1    1    4    7   10   13
ligne2    2    5    8   11   14
ligne3    3    6    9   12   15

A[1, 3]

ligne1 
     7

A[, 2]

ligne1 ligne2 ligne3 
     4      5      6

A[2, ]

[1]  2  5  8 11 14

A[1:3, c(2, 5)]

       [,1] [,2]
ligne1    4   13
ligne2    5   14
ligne3    6   15

A[1:3, -c(2, 5)]

       [,1] [,2] [,3]
ligne1    1    7   10
ligne2    2    8   11
ligne3    3    9   12

`cbind() / rbind()`

Pour concaténer deux matrices, on peut utiliser les fonctions rbind() ou cbind().

       [,1] [,2] [,3] [,4] [,5]
ligne1    1    4    7   10   13
ligne2    2    5    8   11   14
ligne3    3    6    9   12   15

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    6    7    8    9   10
[3,]   11   12   13   14   15

cbind(A, B)

       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
ligne1    1    4    7   10   13    1    2    3    4     5
ligne2    2    5    8   11   14    6    7    8    9    10
ligne3    3    6    9   12   15   11   12   13   14    15

rbind(A, B)

       [,1] [,2] [,3] [,4] [,5]
ligne1    1    4    7   10   13
ligne2    2    5    8   11   14
ligne3    3    6    9   12   15
          1    2    3    4    5
          6    7    8    9   10
         11   12   13   14   15

Fonctions utiles

Dimension d’une matrice

dim(A)

[1] 3 5

Nombre de lignes et de colonnes

nrow(A)

[1] 3

ncol(A)

[1] 5

Transposée et déterminant d’une matrice

t(A)

     ligne1 ligne2 ligne3
[1,]      1      2      3
[2,]      4      5      6
[3,]      7      8      9
[4,]     10     11     12
[5,]     13     14     15

det(A[, 3:5])

[1] 0

Inversion d’une matrice

solve(A[1:2, 2:3])

        ligne1    ligne2
[1,] -2.666667  2.333333
[2,]  1.666667 -1.333333

Matrice diagonale et diagonale d’une matrice

diag(A)

[1] 1 5 9

diag(1:5)

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    2    0    0    0
[3,]    0    0    3    0    0
[4,]    0    0    0    4    0
[5,]    0    0    0    0    5

Matrice de booléens

A > 5

        [,1]  [,2] [,3] [,4] [,5]
ligne1 FALSE FALSE TRUE TRUE TRUE
ligne2 FALSE FALSE TRUE TRUE TRUE
ligne3 FALSE  TRUE TRUE TRUE TRUE

A[A < 5] <- 0
A

       [,1] [,2] [,3] [,4] [,5]
ligne1    0    0    7   10   13
ligne2    0    5    8   11   14
ligne3    0    6    9   12   15

Quelques autres fonctions sur les matrices

colSums(A)

[1]  0 11 24 33 42

apply(A, 2, sum)

[1]  0 11 24 33 42

rowSums(A)

ligne1 ligne2 ligne3 
    30     38     42

apply(A, 1, sum)

ligne1 ligne2 ligne3 
    30     38     42

rowMeans(A)

ligne1 ligne2 ligne3 
   6.0    7.6    8.4

apply(A, 1, mean)

ligne1 ligne2 ligne3 
   6.0    7.6    8.4

apply(A, 1, max)

ligne1 ligne2 ligne3 
    13     14     15

Remarque : on reverra dans la section Programmation la fonction apply() qui permet en particulier d’éviter les boucles for.

Opérations

Attention à la multiplication matricielle %*% et la multiplication terme à terme *!

Opérations terme à terme de 2 matrices

A + B

       [,1] [,2] [,3] [,4] [,5]
ligne1    1    2   10   14   18
ligne2    6   12   16   20   24
ligne3   11   18   22   26   30

A * B

       [,1] [,2] [,3] [,4] [,5]
ligne1    0    0   21   40   65
ligne2    0   35   64   99  140
ligne3    0   72  117  168  225

Multiplication de matrices

t(B) %*% A

     [,1] [,2] [,3] [,4] [,5]
[1,]    0   96  154  208  262
[2,]    0  107  178  241  304
[3,]    0  118  202  274  346
[4,]    0  129  226  307  388
[5,]    0  140  250  340  430

Multiplication par un scalaire

5 * A

       [,1] [,2] [,3] [,4] [,5]
ligne1    0    0   35   50   65
ligne2    0   25   40   55   70
ligne3    0   30   45   60   75

Exercice

Enoncé

Créer la matrice $A=\left(\begin{array}{c c c } 3 & 3 & 3\\ 4 & 4 & 4\\ 5 & 5 & 5\end{array}\right).$
Ajouter 2 à tous les éléments de $A$.
Créer la matrice $B$ en ajoutant la ligne $(1,2,3)$ à $A$, puis la colonne $(1,1,1,1)'$. Déterminer la dimension de $B$.
Extraire de $B$ la sous-matrice $C$ composée des deux premières colonnes et des deux dernières lignes. Calculer sa transposée et son déterminant. Inverser cette sous-matrice $C$.

Correction

Question 1

A = matrix(c(rep(3, 3), rep(4, 3), rep(5, 3)), nrow = 3, byrow = T)
A

     [,1] [,2] [,3]
[1,]    3    3    3
[2,]    4    4    4
[3,]    5    5    5

Question 2

A + 2

     [,1] [,2] [,3]
[1,]    5    5    5
[2,]    6    6    6
[3,]    7    7    7

Question 3

B = rbind(A, 1:3)
B = cbind(B, rep(1, 4))
dim(B)

[1] 4 4

     [,1] [,2] [,3] [,4]
[1,]    3    3    3    1
[2,]    4    4    4    1
[3,]    5    5    5    1
[4,]    1    2    3    1

Question 4

C = B[3:4, 1:2]
C

     [,1] [,2]
[1,]    5    5
[2,]    1    2

t(C)

     [,1] [,2]
[1,]    5    1
[2,]    5    2

det(C)

[1] 5

solve(C)

     [,1] [,2]
[1,]  0.4   -1
[2,] -0.2    1

C %*% solve(C)

     [,1] [,2]
[1,]    1    0
[2,]    0    1

Les tableaux (array)

Les tableaux sont des matrices de dimensions supérieures à 2. On peut les générer à partir de la commande array(vec,c(n,p,q,...)) où vec est le vecteur contenant les éléments du tableau et l’argument c(n,p,q,…) désigne les dimensions du tableau: $n$ lignes, $p$ colonnes, $q$ matrices, …

`array()`

E = array(c(1:8, rep(1, 8), seq(0, 1, len = 8)), dim = c(2, 4, 3))
E

, , 1

     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8

, , 2

     [,1] [,2] [,3] [,4]
[1,]    1    1    1    1
[2,]    1    1    1    1

, , 3

          [,1]      [,2]      [,3]      [,4]
[1,] 0.0000000 0.2857143 0.5714286 0.8571429
[2,] 0.1428571 0.4285714 0.7142857 1.0000000

E[, , 1]

     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8

Fonctions usuelles

dim(E)

[1] 2 4 3

length(E)

[1] 24

nrow(E)

[1] 2

ncol(E)

[1] 4

aperm(E)

, , 1

     [,1]      [,2]      [,3]      [,4]
[1,]    1 3.0000000 5.0000000 7.0000000
[2,]    1 1.0000000 1.0000000 1.0000000
[3,]    0 0.2857143 0.5714286 0.8571429

, , 2

          [,1]      [,2]      [,3] [,4]
[1,] 2.0000000 4.0000000 6.0000000    8
[2,] 1.0000000 1.0000000 1.0000000    1
[3,] 0.1428571 0.4285714 0.7142857    1

E + 10

, , 1

     [,1] [,2] [,3] [,4]
[1,]   11   13   15   17
[2,]   12   14   16   18

, , 2

     [,1] [,2] [,3] [,4]
[1,]   11   11   11   11
[2,]   11   11   11   11

, , 3

         [,1]     [,2]     [,3]     [,4]
[1,] 10.00000 10.28571 10.57143 10.85714
[2,] 10.14286 10.42857 10.71429 11.00000

`apply()`

H = array(1:12, c(2, 3, 2))
H

, , 1

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

, , 2

     [,1] [,2] [,3]
[1,]    7    9   11
[2,]    8   10   12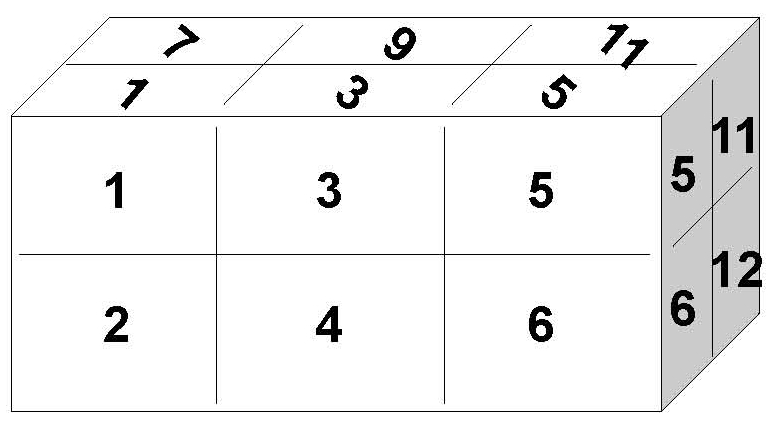

Représentation de H

apply(H, 1, sum)

[1] 36 42

sum(c(1, 3, 5, 7, 9, 11))

[1] 36

apply(H, 2, sum)

[1] 18 26 34

sum(c(1, 2, 7, 8))

[1] 18

apply(H, 3, sum)

[1] 21 57

sum(1:6)

[1] 21

Listes (list)

Une liste est une collection ordonnée d’objets qui peuvent être de nature différente. Les listes sont en particulier utilisées par certaines fonctions (cf section Programmation) pour renvoyer des résultats complexes sous forme d’un seul objet. On utilise la fonction list(nom1=el1,nom2=el2,...) (l’utilisation des noms étant facultative) pour générer une liste. On peut accéder à chaque élément de la liste à l’aide de son index entre double crochets [[...]], ou par son nom précédé du signe $.

Exemples

`list(...)`

x = list("toto", 1:8)
x

[[1]]
[1] "toto"

[[2]]
[1] 1 2 3 4 5 6 7 8

class(x)

[1] "list"

Création d’une liste avec des noms aux éléments

y = list(matrice = matrix(1:15, ncol = 5), vecteur = seq(1, 20, by = 5), texte = "toto",
    scalaire = 8)
y

$matrice
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

$vecteur
[1]  1  6 11 16

$texte
[1] "toto"

$scalaire
[1] 8

Extraction

Extraction d’un élément par son numéro

x[[1]]

[1] "toto"

Attention, cette commande n’est pas possible:

x[[1]] + 1

par contre celle-ci est possible

x[[2]] + 10

[1] 11 12 13 14 15 16 17 18

y[[1]]

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

y$matrice

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

y$vec

[1]  1  6 11 16

y[c("texte", "scalaire")]

$texte
[1] "toto"

$scalaire
[1] 8

Fonctions utiles

names(y)

[1] "matrice"  "vecteur"  "texte"    "scalaire"

length(y)

[1] 4

length(y$vecteur)

[1] 4

cos(y$scal) + y[[2]][1]

[1] 0.8545

summary(y)

         Length Class  Mode     
matrice  15     -none- numeric  
vecteur   4     -none- numeric  
texte     1     -none- character
scalaire  1     -none- numeric

Exercice

Enoncé

Créer une liste contenant le nom de trois matières, les notes de 5 élèves pour chacune de ces matières, l’âge des 5 élèves et la filière (PO) d’appartenance de ces 5 élèves.
Récupérer les notes du 4ème élève
Créer une matrice contenant les notes et l’âge des 5 élèves.

Correction

matiere = c("Maths", "Chimie", "Sport")
age = c(20, 21, 22, 23, 24)
PO = c("MIC", "IMACS", "MIC", "MIC", "IC")
Notes = matrix(c(15, 12, 1, 14, 12, 6, 3, 14, 12, 16, 11, 12, 13, 14, 15), nrow = 5)
A = list(matieres = matiere, Notes = Notes, Age = age, PO = PO)
A

$matieres
[1] "Maths"  "Chimie" "Sport" 

$Notes
     [,1] [,2] [,3]
[1,]   15    6   11
[2,]   12    3   12
[3,]    1   14   13
[4,]   14   12   14
[5,]   12   16   15

$Age
[1] 20 21 22 23 24

$PO
[1] "MIC"   "IMACS" "MIC"   "MIC"   "IC"

A$Notes[4, ]

[1] 14 12 14

B = cbind(A$Notes, A$Age)
B

     [,1] [,2] [,3] [,4]
[1,]   15    6   11   20
[2,]   12    3   12   21
[3,]    1   14   13   22
[4,]   14   12   14   23
[5,]   12   16   15   24

Data frames

Sous R, un data.frame est analogue à une matrice mais le contenu des colonnes peut être ici hétérogène. Un tableau de données est un ensemble de vecteurs rangés colonne par colonne, chaque colonne correspondant à une variable, chaque ligne à un individu. En particulier, lors d’études statistiques, les données à étudier sont souvent représentées par un data.frame sous R. Pour créer un tableau de données, on peut regrouper des variables de même longueur à l’aide de la commande data.frame(nom1=var1,nom2=var2,...). On peut par exemple transformer une matrice en un tableau de données en utilisant la commande as.data.frame(mat).

Exemple

On donne ici quelques exemples à tester sous R pour vous familiariser avec les data.frames. En particulier, vous pouvez découvrir des fonctions utiles dont summary(), attach(), …

`data.frame()`

# Création du data.frame H
taille = runif(12, 150, 180)
masse = runif(12, 50, 90)
sexe = rep(c("M", "F", "F", "M"), 3)
H = data.frame(taille, masse, sexe)
H

     taille    masse sexe
1  171.8216 86.16916    M
2  178.8600 76.40213    F
3  167.7718 85.58736    F
4  173.9192 81.87213    M
5  166.0689 63.14963    M
6  168.5309 73.40069    F
7  162.0680 78.35994    F
8  169.7592 53.30201    M
9  168.3618 68.92062    M
10 157.3739 80.82564    F
11 172.5103 53.20823    F
12 158.9888 56.39809    M

class(H)

[1] "data.frame"

`summary()/head()`

La fonction summary() permet de résumer le contenu des différentes colonnes d’un data.frame.

summary(H)

     taille          masse           sexe          
 Min.   :157.4   Min.   :53.21   Length:12         
 1st Qu.:165.1   1st Qu.:61.46   Class :character  
 Median :168.4   Median :74.90   Mode  :character  
 Mean   :168.0   Mean   :71.47                     
 3rd Qu.:172.0   3rd Qu.:81.09                     
 Max.   :178.9   Max.   :86.17

La fonction head() permet de visualiser les premières lignes d’un data.frame

head(H)

    taille    masse sexe
1 171.8216 86.16916    M
2 178.8600 76.40213    F
3 167.7718 85.58736    F
4 173.9192 81.87213    M
5 166.0689 63.14963    M
6 168.5309 73.40069    F

data.frame / list/matrix

Au travers de ces quelques commandes, vous pouvez voir les analogies entre data.frame, list et matrix mais restez prudent sur la nature de l’objet que vous manipulez!

H[1, ]

    taille    masse sexe
1 171.8216 86.16916    M

H$taille

 [1] 171.8216 178.8600 167.7718 173.9192 166.0689 168.5309 162.0680 169.7592
 [9] 168.3618 157.3739 172.5103 158.9888

H$sexe

 [1] "M" "F" "F" "M" "M" "F" "F" "M" "M" "F" "F" "M"

is.data.frame(H)

[1] TRUE

is.matrix(H)

[1] FALSE

MH = as.matrix(H)
MH

      taille     masse      sexe
 [1,] "171.8216" "86.16916" "M" 
 [2,] "178.8600" "76.40213" "F" 
 [3,] "167.7718" "85.58736" "F" 
 [4,] "173.9192" "81.87213" "M" 
 [5,] "166.0689" "63.14963" "M" 
 [6,] "168.5309" "73.40069" "F" 
 [7,] "162.0680" "78.35994" "F" 
 [8,] "169.7592" "53.30201" "M" 
 [9,] "168.3618" "68.92062" "M" 
[10,] "157.3739" "80.82564" "F" 
[11,] "172.5103" "53.20823" "F" 
[12,] "158.9888" "56.39809" "M"

summary(MH)

    taille             masse               sexe          
 Length:12          Length:12          Length:12         
 Class :character   Class :character   Class :character  
 Mode  :character   Mode  :character   Mode  :character

as.list(H)

$taille
 [1] 171.8216 178.8600 167.7718 173.9192 166.0689 168.5309 162.0680 169.7592
 [9] 168.3618 157.3739 172.5103 158.9888

$masse
 [1] 86.16916 76.40213 85.58736 81.87213 63.14963 73.40069 78.35994 53.30201
 [9] 68.92062 80.82564 53.20823 56.39809

$sexe
 [1] "M" "F" "F" "M" "M" "F" "F" "M" "M" "F" "F" "M"

`attach()/detach()`

La fonction attach() permet d’accéder aux variables d’un data.frame sans appeler le data.frame.

La fonction detach() peut être utilisée pour supprimer la variable d’un data.frame, qui était précédemment attachée avec attach().

rm(taille)
H$taille

 [1] 171.8216 178.8600 167.7718 173.9192 166.0689 168.5309 162.0680 169.7592
 [9] 168.3618 157.3739 172.5103 158.9888

attach(H)
taille

 [1] 171.8216 178.8600 167.7718 173.9192 166.0689 168.5309 162.0680 169.7592
 [9] 168.3618 157.3739 172.5103 158.9888

detach(H)  # taille est alors introuvable

Exercice

Enoncé

On reprend le data.frame $H$ contruit dans la sous-section Exemple.

Extraire la masse des individus dont la taille est supérieure à 160.
Extraire la masse et le sexe de ces mêmes individus.
Extraire la taille des individus de sexe masculin dont la masse est inférieure à 80 (c’est possible en une seule ligne avec &).

Correction

Question 1

H$masse[H$taille > 160]

 [1] 86.16916 76.40213 85.58736 81.87213 63.14963 73.40069 78.35994 53.30201
 [9] 68.92062 53.20823

H[H$taille > 160, 2]

 [1] 86.16916 76.40213 85.58736 81.87213 63.14963 73.40069 78.35994 53.30201
 [9] 68.92062 53.20823

Question 2

H[H$taille > 160, 2:3]

      masse sexe
1  86.16916    M
2  76.40213    F
3  85.58736    F
4  81.87213    M
5  63.14963    M
6  73.40069    F
7  78.35994    F
8  53.30201    M
9  68.92062    M
11 53.20823    F

H[H$taille > 160, c("masse", "sexe")]

      masse sexe
1  86.16916    M
2  76.40213    F
3  85.58736    F
4  81.87213    M
5  63.14963    M
6  73.40069    F
7  78.35994    F
8  53.30201    M
9  68.92062    M
11 53.20823    F

Question 3

H$taille[H$sexe == "M" & H$masse < 80]

[1] 166.0689 169.7592 168.3618 158.9888

H[H$sexe == "M" & H$masse < 80, "taille"]

[1] 166.0689 169.7592 168.3618 158.9888

Premiers graphiques

Nous allons dans cette partie présenter les bases des graphiques en R. Une présentation plus spécifique du package ggplot2 est disponible dans le tutoriel 4 de R avancé.

Gestion des fenêtres graphiques

Pour ouvrir une fenêtre graphique, on utilise x11() sous Unix, windows() sous Windows et quartz() sous MacOS X. La commande dev.list() permet de lister les fenêtres graphiques ouvertes. Il est important de clôturer une fenêtre graphique avec la commande dev.off().

La fonction split.screen permet de partitionner une fenêtre graphique active en plusieurs sous-fenêtres graphiques. Par exemple, split.screen(c(1,2)) divise la fenêtre graphique en 2 parties qu’on sélectionne avec screen(1) et screen(2). On peut également obtenir de telles partitions avec la commande layout ou l’option mfrow de la fonction par().

Fonctions graphiques

En R il faut distinguer les fonctions graphiques principales qui créent une nouvelle fenêtre graphique lors de l’execution avec possibilité d’un titre, d’axes labélisés, … et les fonctions graphiques secondaires qui ont une action sur un graphique déjà existant.

Fonctions graphiques principales

Voici une liste des fonctions principales les plus connues :

Fonction	Description
plot(x)	graphe des valeurs de x (axe des y) ordonnées sur l’axe des x
plot(x, y)	graphe bivarié de x (sur l’axe des x) et y (sur l’axe des y)
pie(x)	graphe en camembert
boxplot(x)	graphe boites à moustaches
pairs(x)	si x est une matrice ou un tableau de données, dessine tous les graphes bivariés entre les colonnes de x
hist(x)	histogramme des fréquences de x
barplot(x)	histogramme des valeurs de x
contour(x,y,z)	courbes de niveau (les données sont interpolées pour tracer les courbes), x et y doivent être des vecteurs et z une matrice telle que dim(z)=c(length(x), length(y))
image(x,y,z)	idem mais les données sont représentées avec des couleurs
persp(x,y,z)	idem mais en perspective

Pour chaque fonction, les options peuvent être trouvées via l’aide. Certaines de ces options sont identiques pour plusieurs fonctions graphiques; voici les principales (avec leurs éventuelles valeurs par défaut) :

option	Description
add=FALSE	si TRUE superpose le graphe au graphe existant (s’il y en a un)
axes=TRUE	si FALSE ne trace pas les axes ni le cadre
type=	le type de graphe qui sera dessiné, p : points, l : lignes, b : points connectés par des lignes, h : lignes verticales,o : idem mais les lignes recouvrent les points, s : escaliers, les données étant représentées par le sommet (par le bas) des lignes verticales
xlim=,ylim=	fixe les limites inférieures et supérieures des axes
xlab=,ylab=	annotations des axes (variables de mode caractère)
main=	titre principal (variable de mode caractère)
sub=	sous-titre (écrit dans une police plus petite)

Fonctions graphiques secondaires

Fonctions graphiques secondaires les plus connues :

Code	Description
points(x,y)	ajoute des points (l’option type= peut être utilisée)
lines(x,y)	idem mais avec des lignes
text(x,y,labels,…)	ajoute le texte spécifié par labels aux coordonnées (x,y)
segments(x0,y0,x1,y1)	trace des lignes des points (x0,y0) aux points (x1,y1)
abline(a,b)	trace une ligne de pente b et d’ordonnée à l’origine a
abline(h=y)	trace une ligne horizontale sur l’ordonnée y
abline(v=x)	trace une ligne verticale sur l’abscisse x
rect(x1,y1,x2,y2)	trace un rectangle délimité à gauche par x1, à droite par x2,en bas par y1 et en haut par y2
polygon(x,y)	trace un polygone reliant les points dont les coordonnées sont données par x et y
legend(x,y,legend)	ajoute la légende au point de coordonnées (x,y) avec les symboles donnés par legend
title()	ajoute un titre et optionnellement un sous-titre
axis(side, vect)	ajoute un axe en bas (side=1), à gauche (2), en haut (3) ou à droite (4) ; vect (optionnel) indique les abscisses (ou ordonnées) où les graduations seront tracées
box()	ajoute un cadre autour du graphe

Exemples

Exemple 1

x = seq(-10, 10, l = 50)
# 2 graphiques
par(mfrow = c(1, 2))
# premier graphique
plot(x, sin(x), type = "l", col = 1, main = "sinus")
abline(v = 0, col = "blue", lwd = 5, lty = 3)
abline(h = sin(0.7), col = 3)
text(-5, -0.5, "texte", font = 3)
# deuxieme graphique
plot(x, cos(x), type = "b", col = 3, xlab = "Abscisses")
points(x, cos(x), type = "l")
points(0, 1, pch = "o", cex = 3, col = "blue")
lines(c(-5, 5), c(0, 0), lty = 2, col = 2)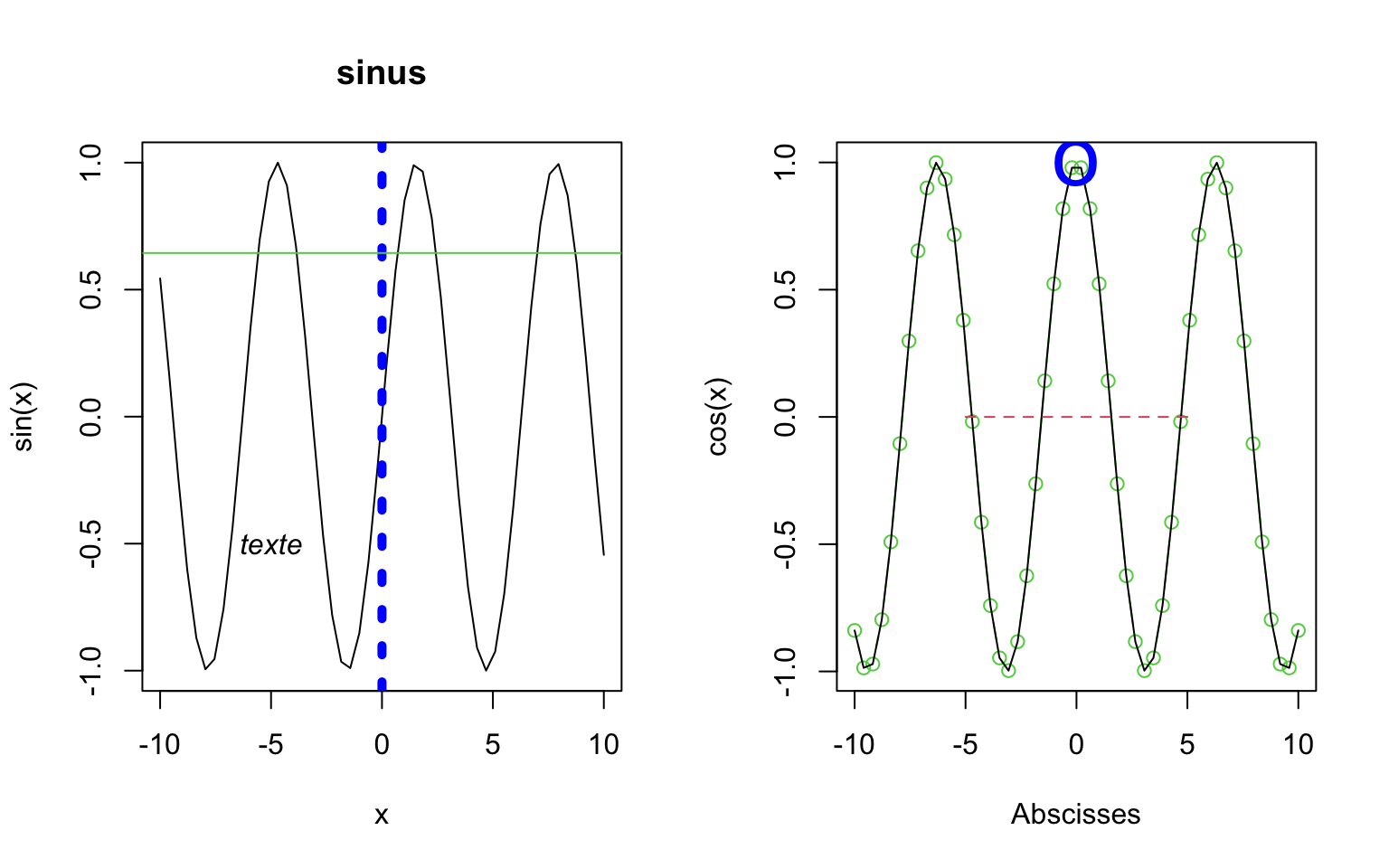

Exemple 2

data(iris)
par(mfrow = c(2, 2))
plot(iris[, 1], iris[, 2], xlab = "Sepal Length", ylab = "Sepal Width", main = "Iris data",
    col = "red", type = "p")
points(iris[iris$Species == "setosa", 1], iris[iris$Species == "setosa", 2], col = "green",
    pch = 20)
hist(iris[, 1], xlab = "Sepal Length", main = "Histogramme de la variable Sepal Length")
boxplot(iris[, 1:4], las = 2)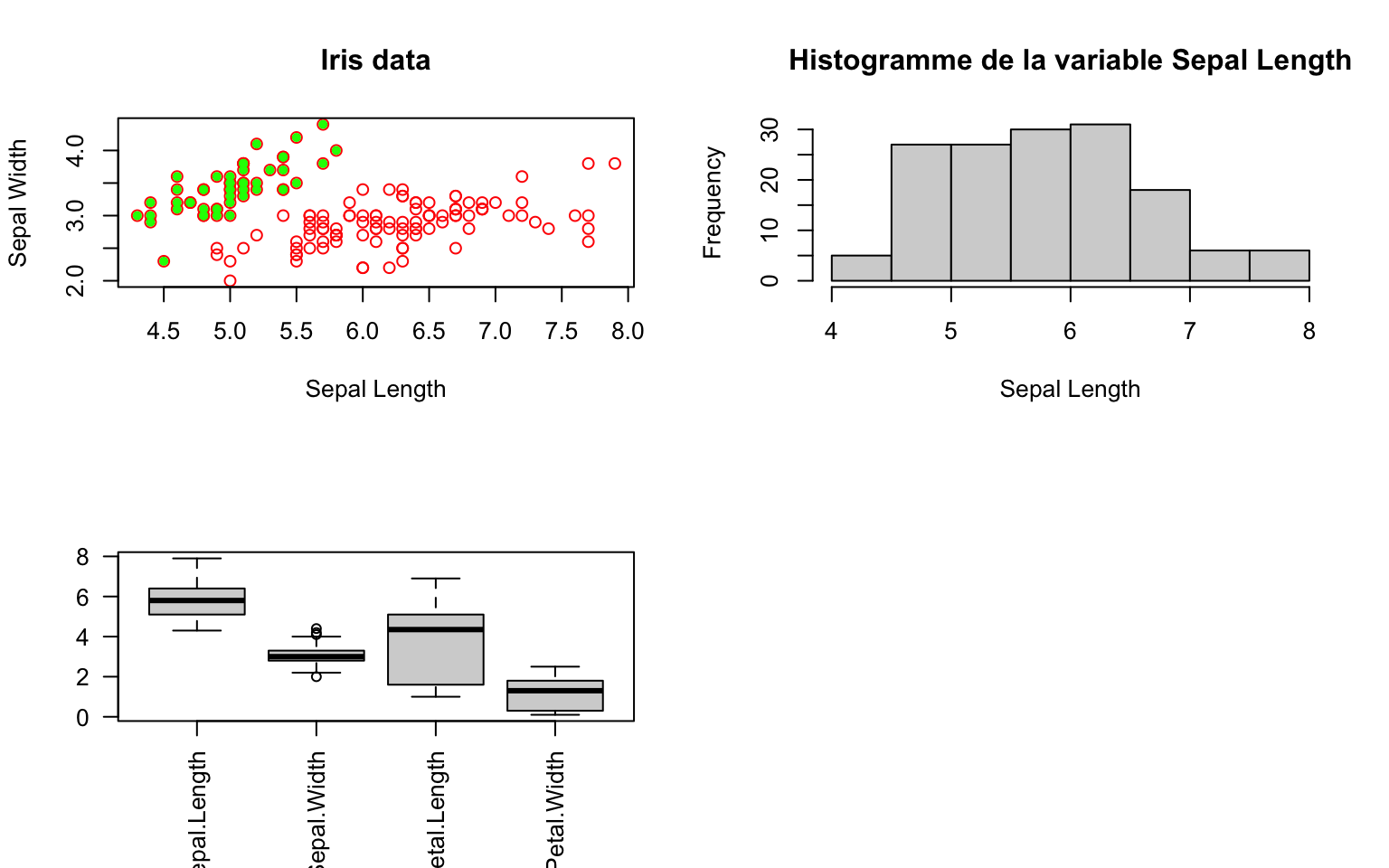

pairs(iris[, 1:4])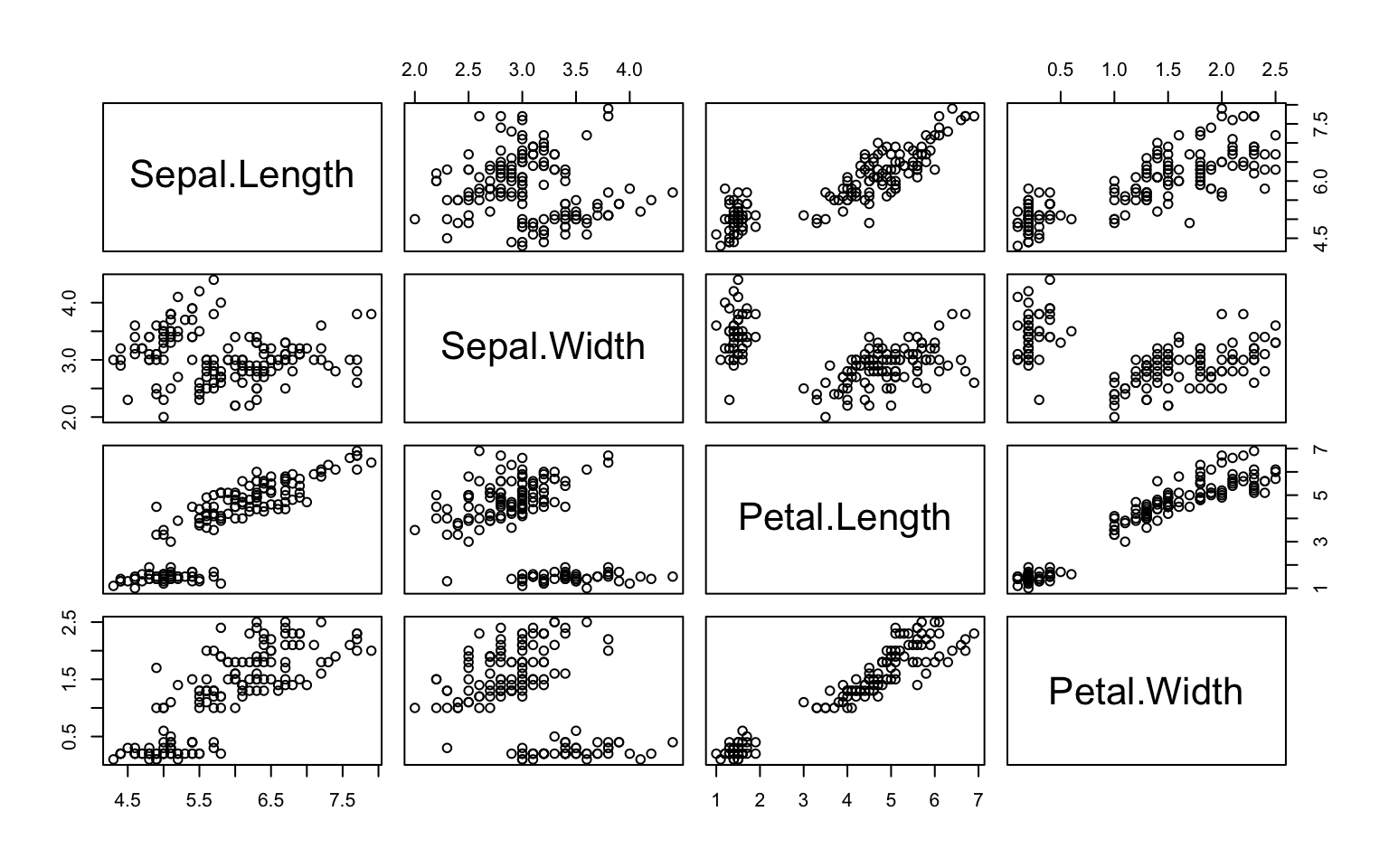

par(mfrow = c(2, 2))
pie(table(iris[, 5]))
pie(table(iris[, 5]), clockwise = T)
barplot(table(iris[, 5]))
stripchart(iris, las = 1)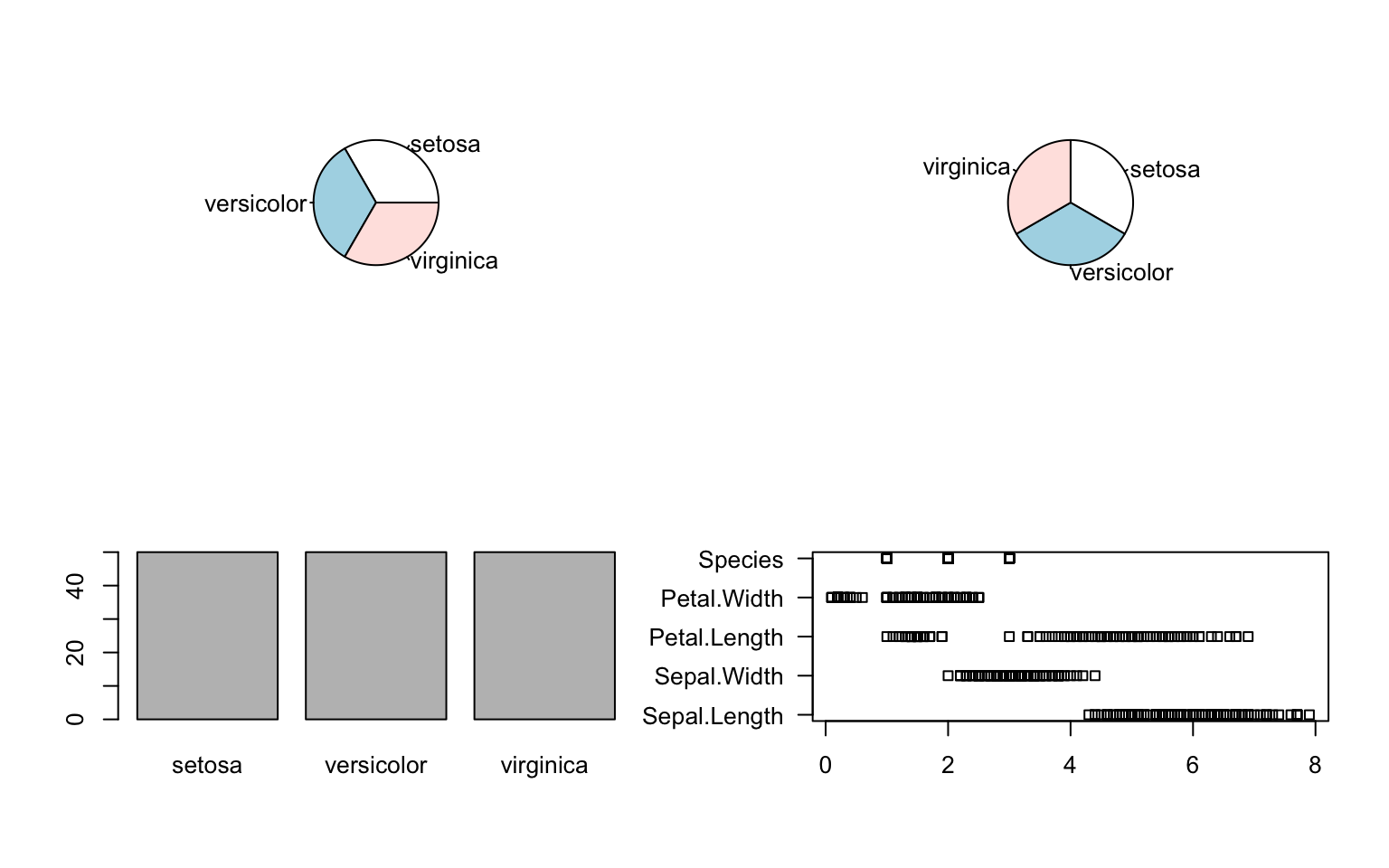

Exemple 3

M = matrix(1:100, ncol = 10)
image(M)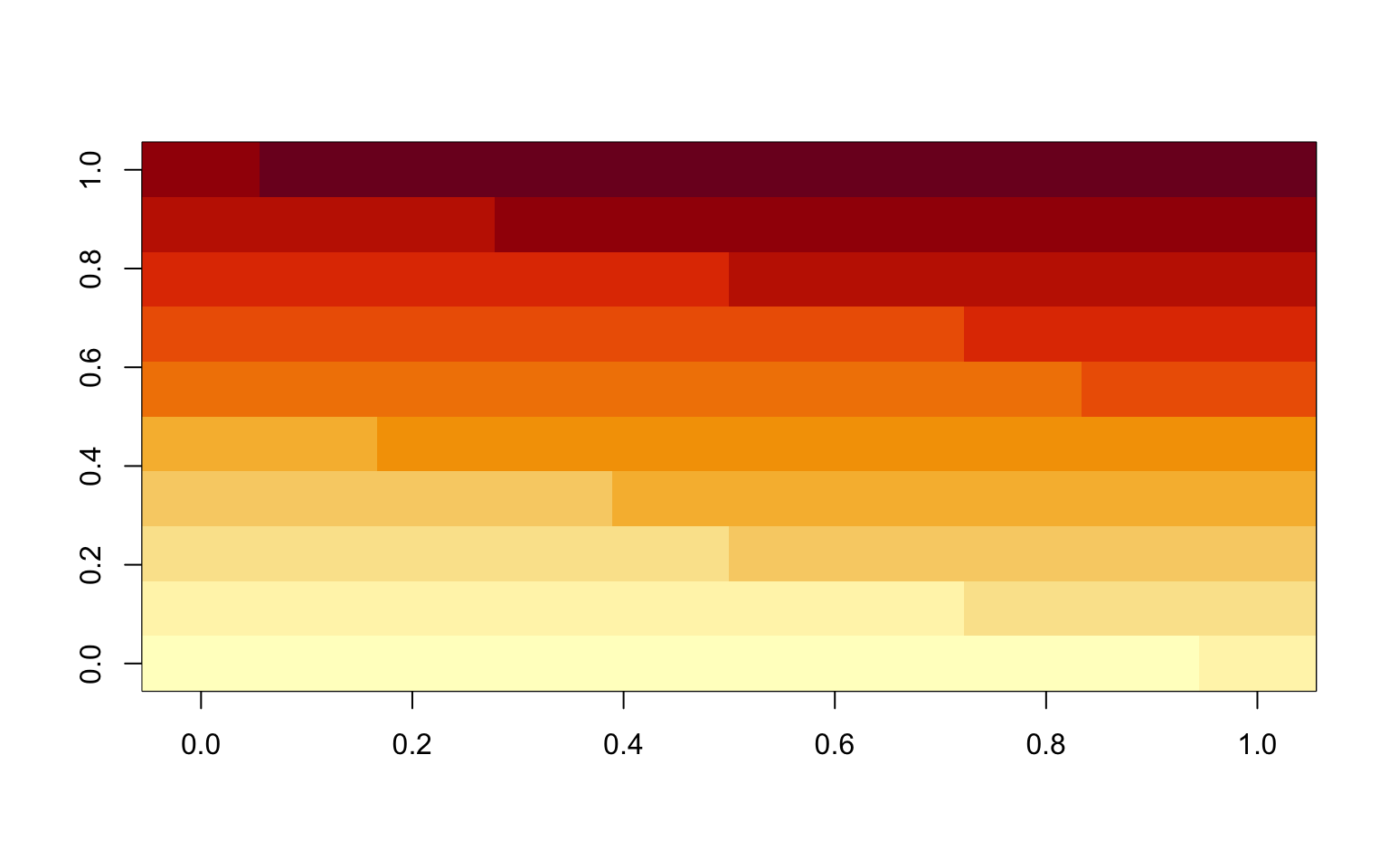

x = seq(-10, 10, length = 30)
y = x
f = function(x, y) {
    r = sqrt(x^2 + y^2)
    10 * sin(r)/r
}
z = outer(x, y, f)
z[is.na(z)] = 1
persp(x, y, z)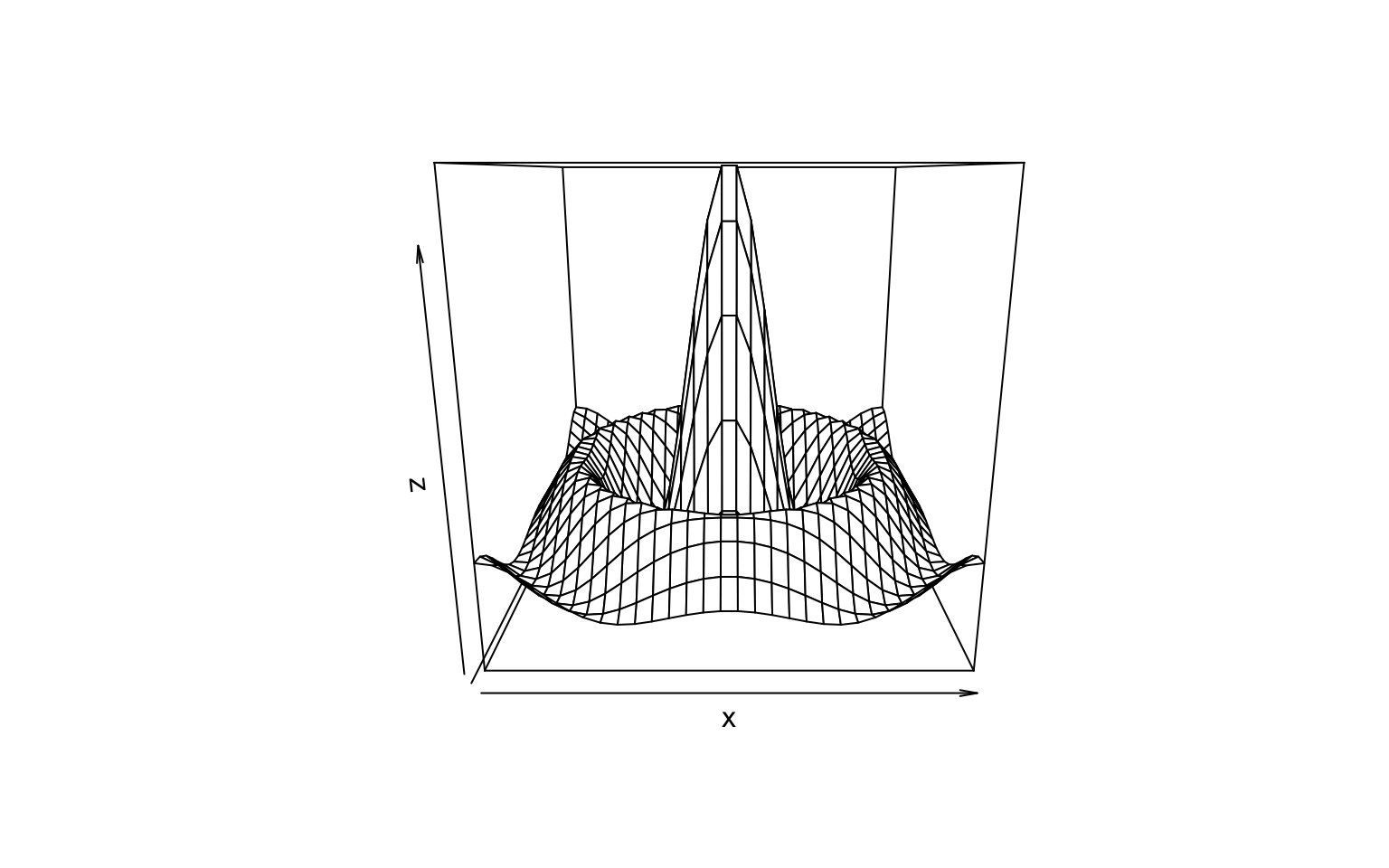

persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")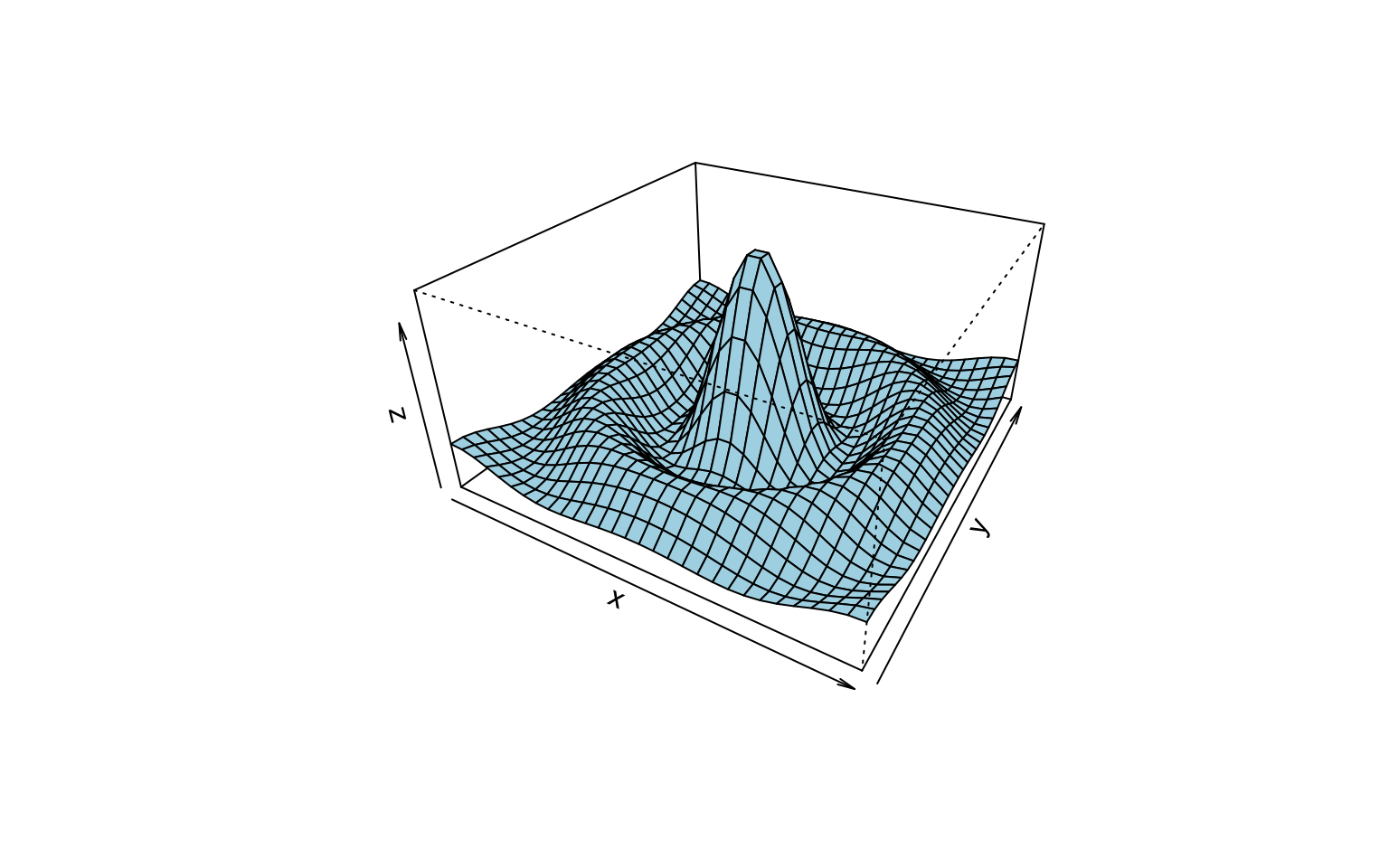

image(x, y, z)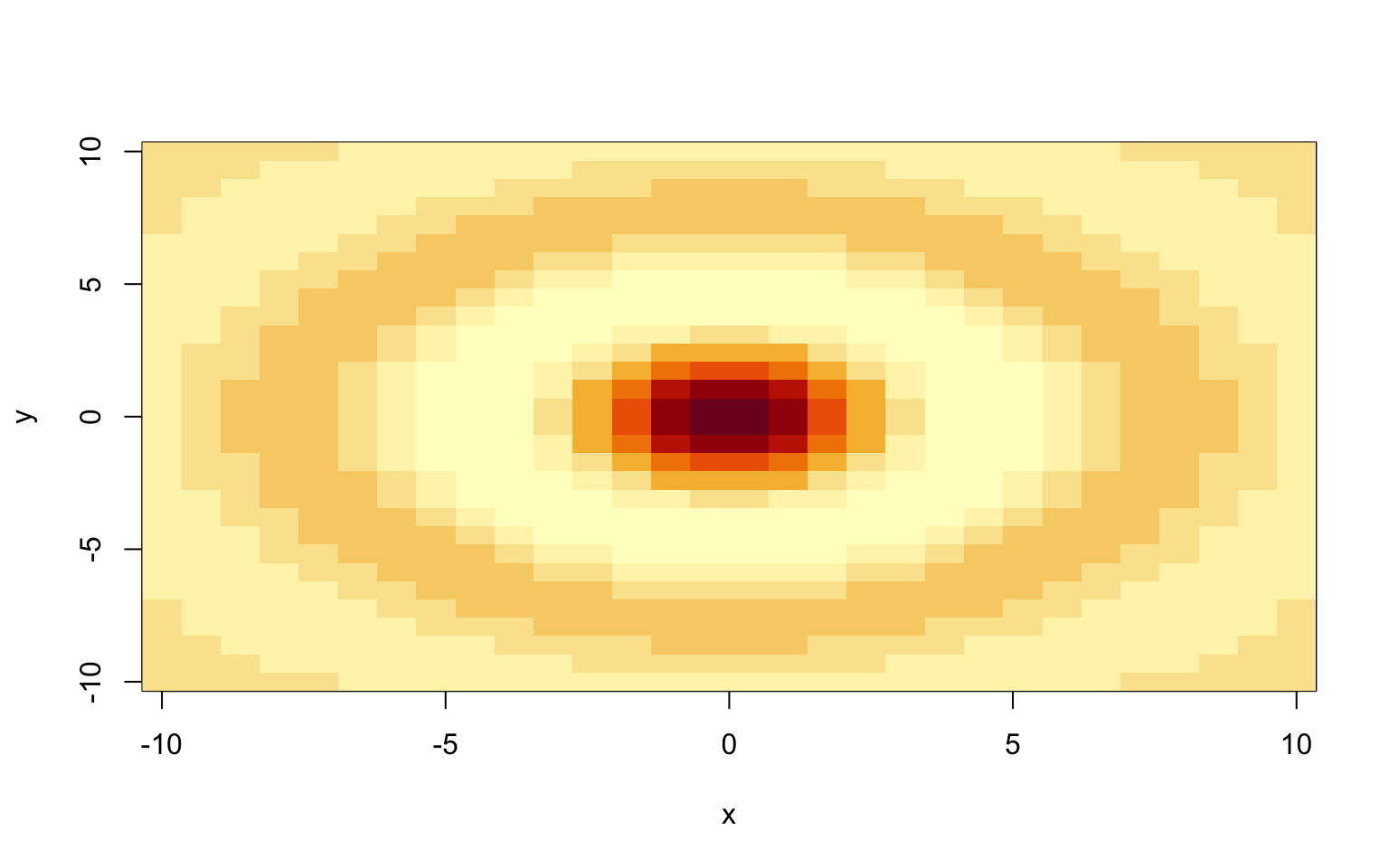

contour(x, y, z)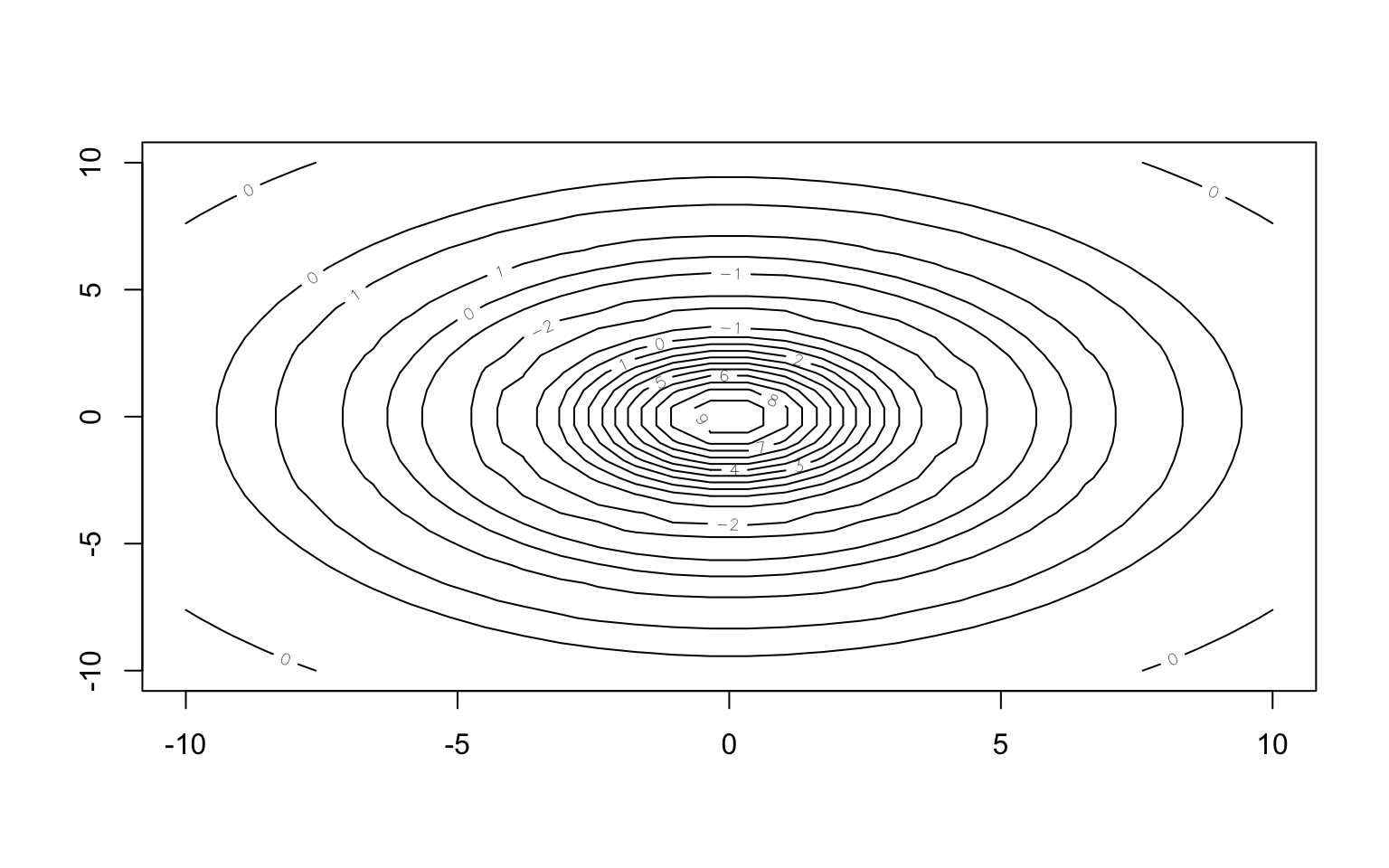

filled.contour(x, y, z)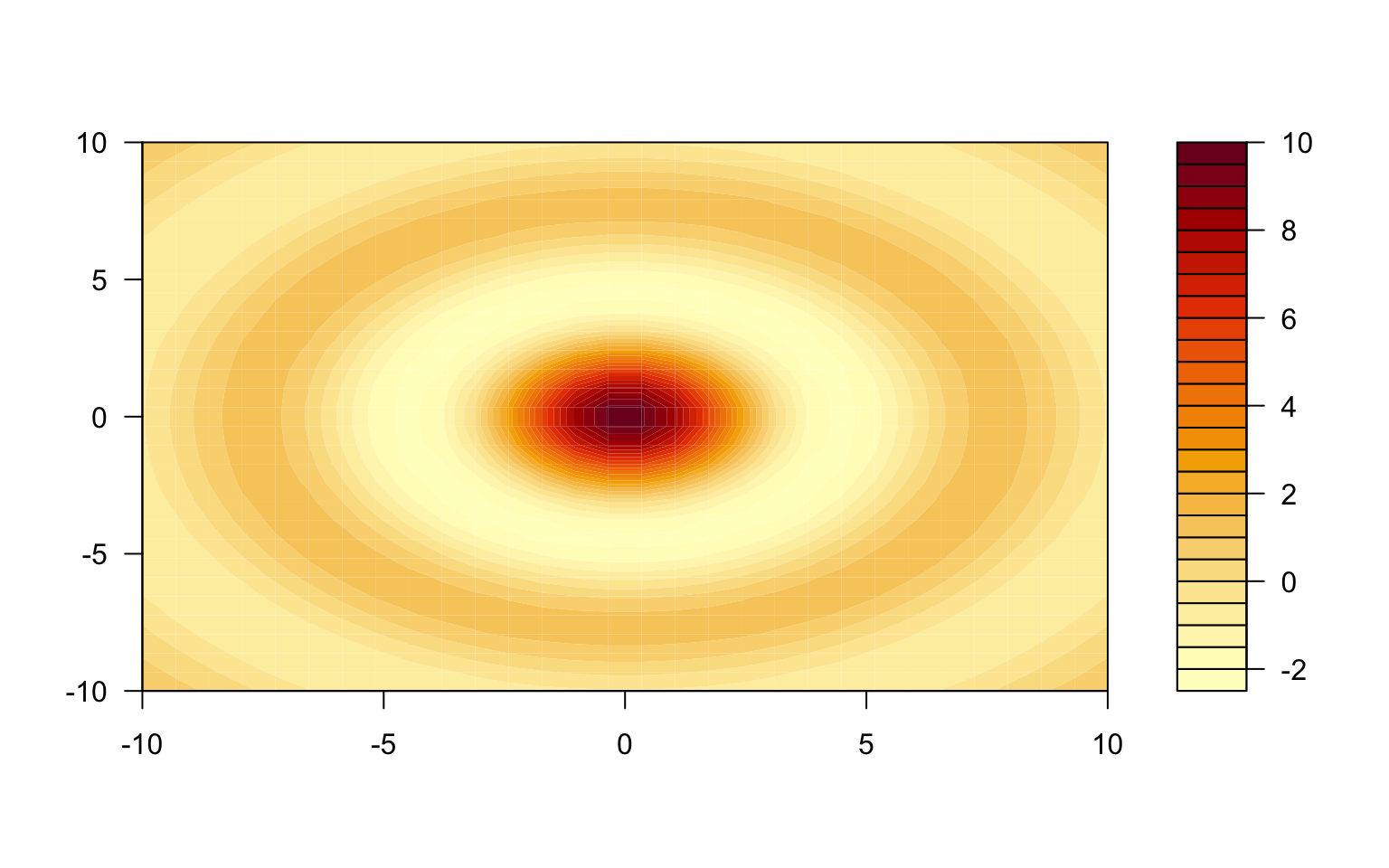

image(x, y, z)
contour(x, y, z, add = T)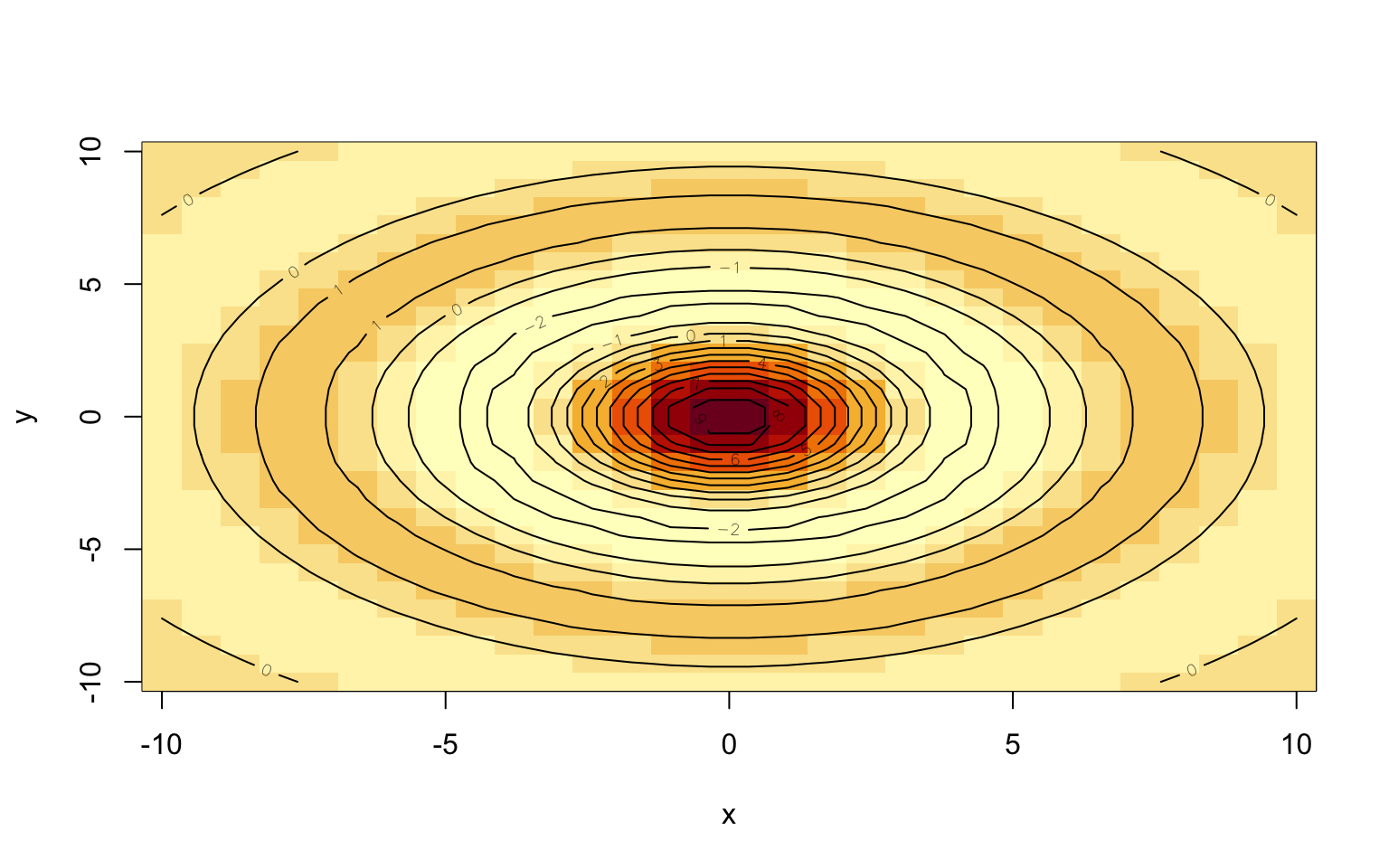

Exercices

Enoncé 1

Tracer la fonction arctangente entre $-10$ et $10$
Ajouter les deux asymptotes en $-\infty$ et $+\infty$ en bleu
Ajouter les points sur la courbe pour $x=-\pi$, $0$ et $\pi$ en vert
Ajouter la tangente en zéro en pointillés rouge

Enoncé 2

Charger les données “airquality” disponible sous R à l’aide de data()
Utiliser la commande pairs() pour visualiser variable contre variable
Créer une fenêtre graphique contenant les boxplots des 4 premières variables, l’histogramme de la variable Ozone, le graphique en camembert de la variable Month, et le graphique représentant la variable Wind contre la variable Ozone avec une couleur par mois et une légende.

Enoncé 3

Saurez-vous tracer la “tête à Toto” ?

Correction

Exercice 1 :

x = seq(-10, 10, 0.01)
plot(x, atan(x), type = "l", ylim = c(-pi/2 - 0.2, pi/2 + 0.2))
abline(h = pi/2, col = "blue")
abline(h = -pi/2, col = "blue")
points(c(-pi, 0, pi), c(atan(-pi), 0, atan(pi)), pch = 20, col = "green")
lines(c(-5, 5), c(-5, 5), lty = 2, col = "red")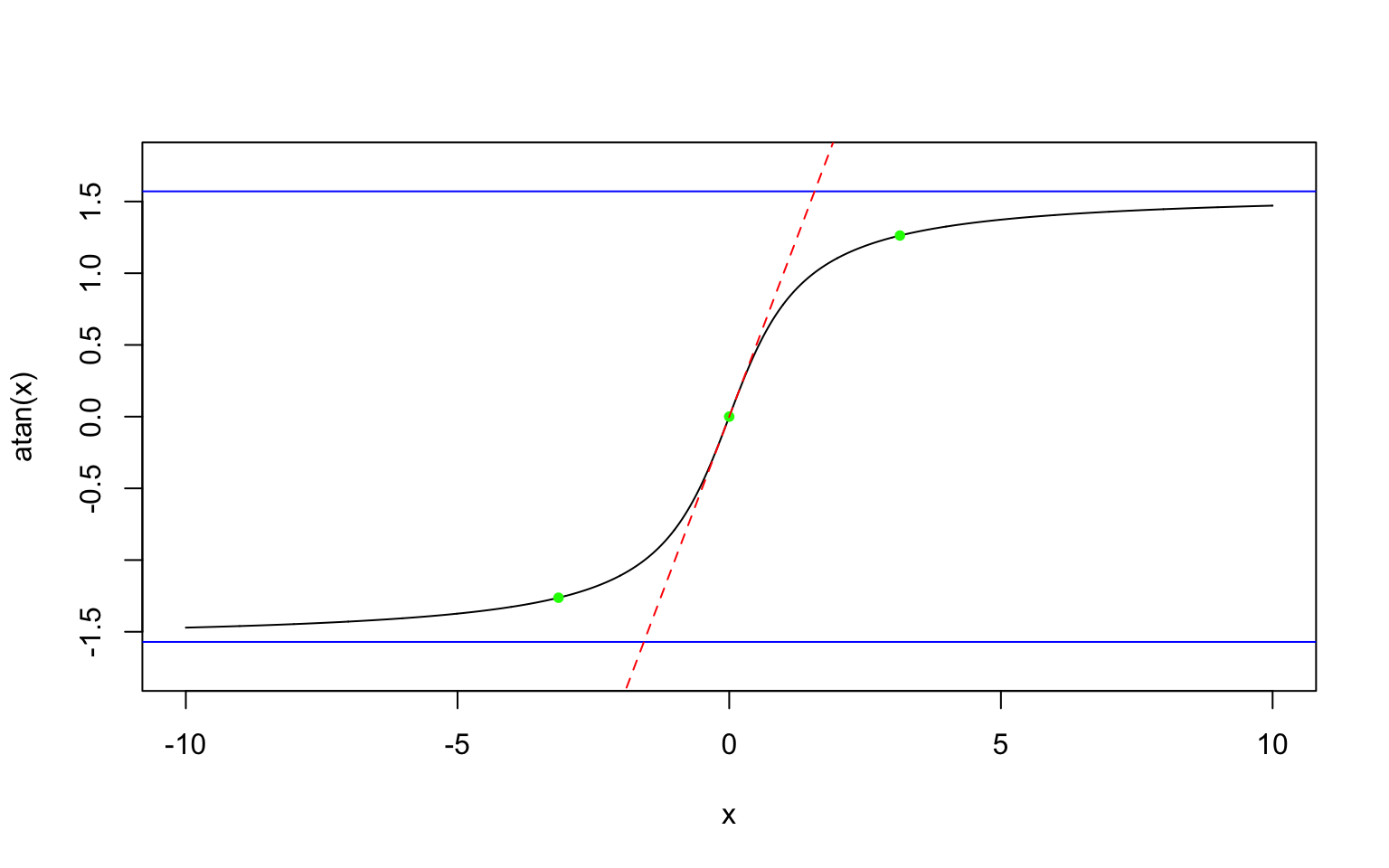

Exercice 2 :

# Question 1
data(airquality)
head(airquality)

  Ozone Solar.R Wind Temp Month Day
1    41     190  7.4   67     5   1
2    36     118  8.0   72     5   2
3    12     149 12.6   74     5   3
4    18     313 11.5   62     5   4
5    NA      NA 14.3   56     5   5
6    28      NA 14.9   66     5   6

# Question 2
pairs(airquality)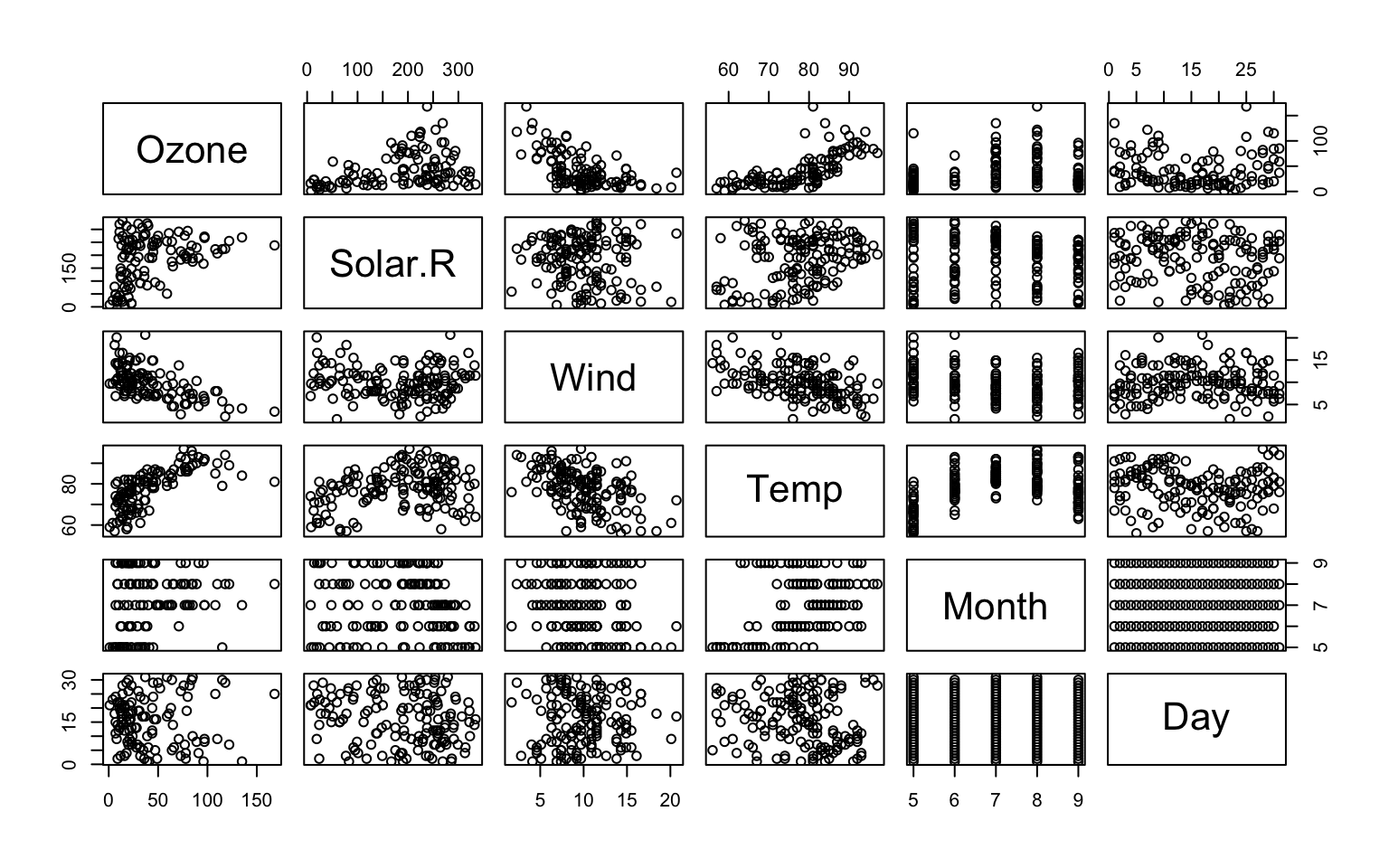

# Question 3
par(mfrow = c(2, 2))
boxplot(airquality[, 1:4])
pie(table(airquality[, "Month"]))
plot(airquality$Ozone, airquality$Wind, col = airquality$Month, pch = 20)
legend(x = "topright", legend = unique(airquality$Month), col = 1:length(airquality$Month),
    pch = 20)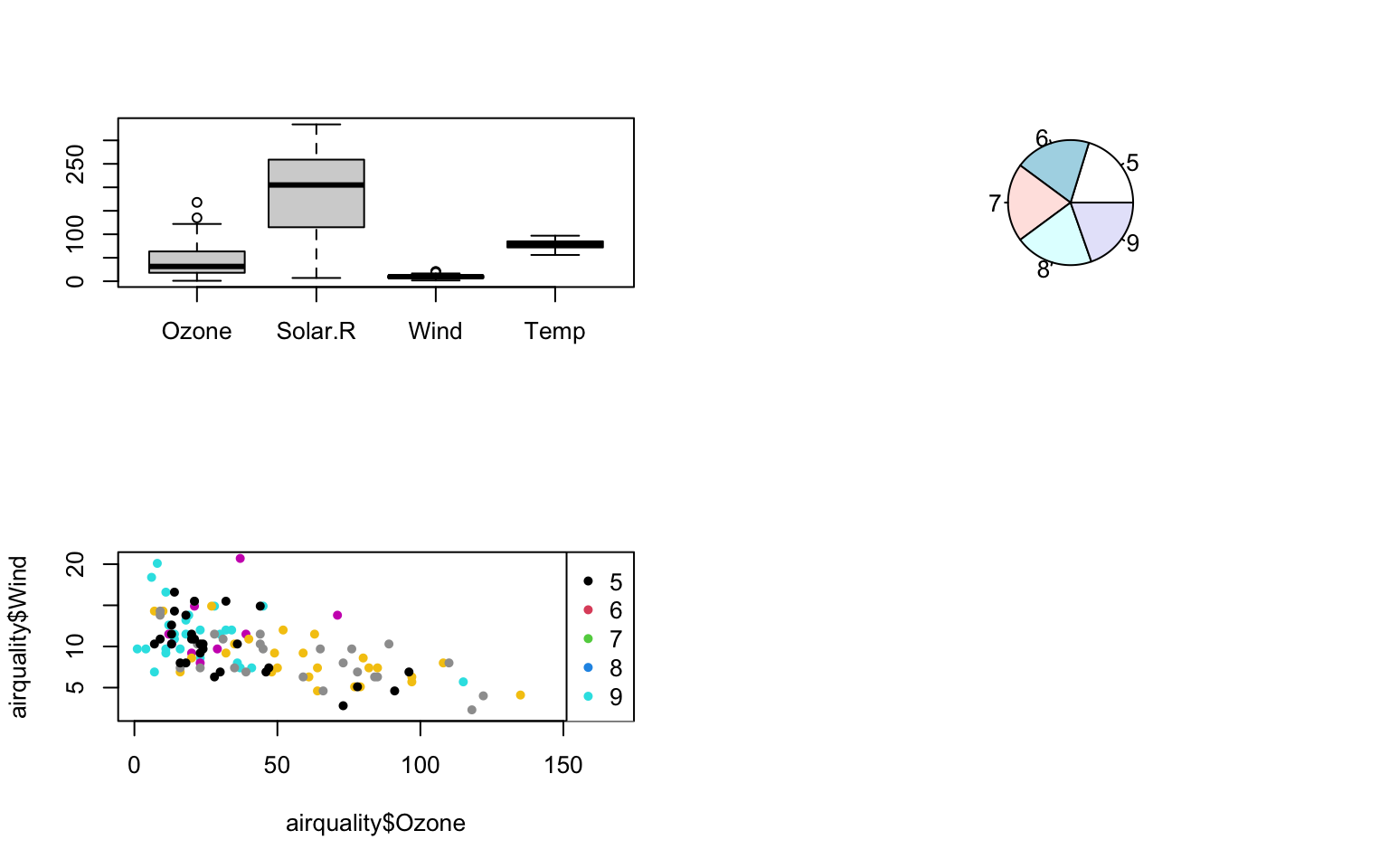

Exercice 3 :

plot(0, 0, xlim = c(-15, 15), ylim = c(-15, 15), type = "n", axes = FALSE, xlab = "",
    ylab = "")
points(0, 0, pch = "+", cex = 4)
points(c(-4, 4), c(5, 5), pch = "O", cex = 4)
lines(c(-3, 3), c(-5, -5), lwd = 3)
lines(c(-3, 3), c(-6, -6), lwd = 3)
lines(10 * sin(0:360 * pi/180), 10 * cos(0:360 * pi/180), lwd = 5)
# En option, le chapeau
lines(c(-12, 12), c(10, 10), lwd = 3)
rect(-6, 10, 6, 14, border = 1, lwd = 3, col = 1)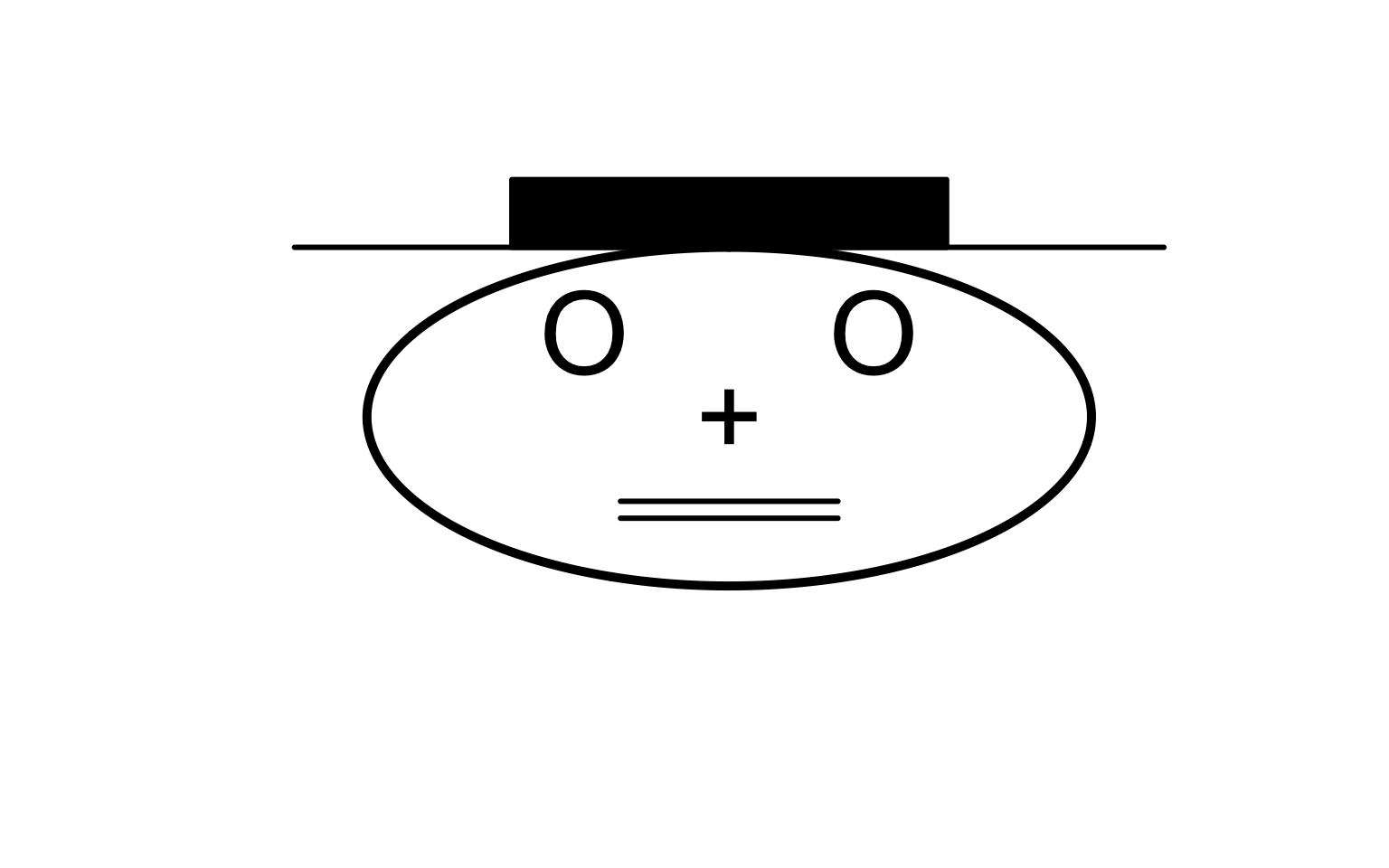

Exportation de graphiques

Dans l’environnement Windows, une première solution consiste à copier le graphique (menu Fichier > Copier vers le presse-papier). Le graphique ainsi placé dans le presse-papier peut ensuite être collé dans le logiciel de son choix.

Pour sauvegarder le graphique dans un fichier, on utilisera dans le menu Fichier la rubrique Sauver sous. Plusieurs formats sont disponibles : vectoriel (métafichier), postscript, pdf, png, bmp, jpeg.

Une autre façon de procéder est d’utiliser les fonctions associées à la sauvegarde de fichiers graphiques : bmp(), jpeg(), png(), pdf(), postscript().

Cette procédure est également utile en environnement Windows lorsque l’on souhaite sauver un graphique tracé lors du déroulement d’une fonction.

On peut également utiliser la commande dev.print(...) pour sauvegarder une figure en pdf ou eps.

Programmation

Cette partie est consacrée à la création des fonctions, les instructions de contrôle, la syntaxe des itérations et la fonction apply() (et ses dérivées).

Créer une fonction

Il est possible sous R de construire ses propres fonctions. Il est conseillé d’écrire sa fonction dans un fichier nomfonction.R, puis dans la console, de charger la fonction grâce à la commande >source("nomfonction.R") et de l’utiliser. On peut également écrire directement la fonction dans la console. De manière générale, la définition d’une nouvelle fonction passe par l’expression suivante :

nomfonction=function(arg1[=exp1],arg2[=exp2],...){
    bloc d instructions
    sortie = ...
    return(sortie)
}

Les accolades signalent le début et la fin du code source de la fonction, les crochets indiquent le caractère facultatif des valeurs par défaut des arguments. L’objet sortie contient le ou les résultats retournés par la fonction, on peut en particulier utiliser une liste pour retourner plusieurs résultats.

Exemples

Exemple 1

MaFonction = function(x) {
    x + 2
}
MaFonction

function(x) {
    x + 2
}

MaFonction(3)

[1] 5

x = MaFonction(4)
x

[1] 6

Fonction2 = function(a, b = 7) {
    a + b
}
Fonction2(2, b = 3)

[1] 5

Fonction2(5)

[1] 12

Exemple 2

Fonction retournant le périmètre et la surface d’un cercle à partir de son rayon :

CalculsCercle = function(r) {
    p = 2 * pi * r
    s = pi * r * r
    resultats = list(perimetre = p, surface = s)
    return(resultats)
}
res = CalculsCercle(3)
res

$perimetre
[1] 18.84956

$surface
[1] 28.27433

res$surf

[1] 28.27433

Exercice :

Enoncé

Construire une fonction qui prend en argument deux réels x et y et qui retourne l’arrondi à 3 chiffres après la virgule de $x^2 + y$. Vous pouvez vous aider de la fonction round().
Construire une fonction qui permet de calculer la densité de probabilité d’une loi normale de moyenne $m$ et d’écart-type $s$ au point $x$.

Correction

Question 1

arrond = function(x, y) {
    s = round((x^2) + y, 3)
    return(s)
}
arrond(1.23456, 9.8765)

[1] 11.401

Question 2

densitegauss = function(m, sigma, x) {
    f = (1/(sqrt(2 * pi) * sigma)) * exp(-((x - m)^2)/(2 * sigma^2))
    return(f)
}
densitegauss(1, 2, 1.2)

[1] 0.1984763

dnorm(1.2, 1, 2)

[1] 0.1984763

Structures de contrôle et itérations

Instructions conditionnelles

La syntaxe if(condition){instructions} permet de calculer les instructions uniquement si la condition est vraie. Le code if(condition){ A }else { B } calcule les instructions A si la condition est vraie et les instructions B sinon. On peut également utiliser ifelse.

Dans l’exemple suivant, les deux commandes sont équivalentes :

if (x > 0) {
    y = x * log(x)
} else {
    y = 0
}
y = ifelse(x > 0, x * log(x), 0)

Exercice

Enoncé

Soit $X$ une variable aléatoire de loi de Poisson de paramètre $\lambda=2$. Écrire une fonction qui prend en argument un réel $x$ et qui retourne la probabilité que $X$ soit égal à $x$.

Correction

Question 1

Poiss = function(x) {
    p = NULL
    if ((x >= 0) & (round(x) == x)) {
        p = exp(-2) * (2^x)/(factorial(x))
    } else {
        print("x n'est pas un entier")
    }
    return(p)
}

Poiss(3)

[1] 0.180447

dpois(3, 2)

[1] 0.180447

Poiss(1.5)

[1] "x n'est pas un entier"

NULL

Itérations

On utilise les boucles pour exécuter plusieurs fois une instruction ou un bloc d’instructions. Les trois types de boucle sont :

la boucle for : for(var in seq){ commandes }
la boucle while : while(cond){ commandes }
la boucle repeat : repeat { commandes ; if (cond) break }

Dans une boucle for, le nombre d’itérations est fixe alors qu’il peut être infini pour les boucles while et repeat !

Exemples

Pour illustrer les trois types de boucle, on a codé de trois façons différentes la somme des éléments d’un vecteur x ce qui correspond à la fonction sum() de R.

Exemple `for()`

somme1 = function(x) {
    t = 0
    for (i in 1:length(x)) t = t + x[i]
    return(t)
}

x = seq(1:10)
somme1(x)

[1] 55

sum(x)

[1] 55

Exemple `while()`

somme2 = function(x) {
    t = 0
    i = 1
    while (i <= length(x)) {
        t = t + x[i]
        i = i + 1
    }
    return(t)
}
x = seq(1:10)
somme2(x)

[1] 55

sum(x)

[1] 55

Exemple `repeat()`

somme3 = function(x) {
    t = 0
    i = 1
    repeat {
        t = t + x[i]
        i = i + 1
        if (i > length(x))
            break
    }
    return(t)
}

x = seq(1:10)
somme3(x)

[1] 55

sum(x)

[1] 55

Exercice

Enoncé

Écrire une fonction ma.variance qui calcule la variance empirique corrigée pour un vecteur $x = (x_1, . . . , x_n)$. Comparer avec la fonction prédéfinie var().
Écrire une fonction qui calcule les $n$ premiers termes de la suite de Fibonacci ($u_1=0, u_2=1, \forall n>2, u_n=u_{n-1}+u_{n-2}$)
Ecrire une fonction qui prend en entrée un entier $x$ et retourne sa factorielle $x!$ avec une boucle for() puis avec une boucle while().

Correction

Question 1

ma.variance = function(x) {
    v = 0
    m = 0
    n = length(x)
    for (i in 1:n) {
        v = v + x[i]^2
        m = m + x[i]
    }
    vv = (v - ((m^2)/n))/(n - 1)
    return(vv)
}

x = rnorm(10, 0, 2)
ma.variance(x)

[1] 4.556904

var(x)

[1] 4.556904

Question 2

fibo = function(n) {
    res = rep(0, n)
    res[1] = 0
    res[2] = 1
    for (i in 3:n) {
        res[i] = res[i - 1] + res[i - 2]
    }
    return(res)
}
fibo(10)

 [1]  0  1  1  2  3  5  8 13 21 34

Question 3

facto1 = function(x) {
    res = 1
    for (i in 1:x) {
        res = res * i
    }
    return(res)
}

facto2 = function(x) {
    res = 1
    while (x > 1) {
        res = res * x
        x = x - 1
    }
    return(res)
}

factorial(5)

[1] 120

facto1(5)

[1] 120

facto2(5)

[1] 120

`apply()` et ses variantes

Il est recommandé d’éviter les boucles très chronophages. On peut utiliser pour cela la fonction apply() et ses variantes sapply(), lapply(), tapply() sur des vecteurs ou matrices.

La fonction apply() permet d’appliquer la même fonction FUN sur toutes les lignes (MARGIN=1) ou les colonnes (MARGIN=2) d’une matrice MAT : apply(MAT , MARGIN, FUN).

Les fonctions lapply() et sapply() calculent la même fonction sur tous les éléments d’un vecteur ou d’une liste. La commande lapply(X,FUN, ARG.COMMUN) permet d’appliquer la fonction FUN à tous les éléments du vecteur ou de la liste X. Les valeurs de X sont affectées au premier argument de la fonction FUN. Si la fonction FUN a plusieurs paramètres d’entrée, ils sont spécifiés dans ARG.COMMUN. Cette fonction retourne le résultat sous la forme de listes. sapply() est une fonction similaire à lapply() mais le résultat est retourné sous forme de vecteurs, si possible.

La fonction tapply() applique une fonction FUN sur les sous-groupes d’un vecteur X définis par une variable de type factor GRP : tapply(X,GRP,FUN,...).

Exemples

data(iris)
head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

apply(iris[, 1:4], 2, mean)

Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
    5.843333     3.057333     3.758000     1.199333

apply(iris[, 1:4], 1, mean)

 [1] 2.550 2.375 2.350 2.350 2.550 2.850 2.425 2.525 2.225 2.400 2.700 2.500
[13] 2.325 2.125 2.800 3.000 2.750 2.575 2.875 2.675 2.675 2.675 2.350 2.650
[25] 2.575 2.450 2.600 2.600 2.550 2.425 2.425 2.675 2.725 2.825 2.425 2.400
[37] 2.625 2.500 2.225 2.550 2.525 2.100 2.275 2.675 2.800 2.375 2.675 2.350
[49] 2.675 2.475 4.075 3.900 4.100 3.275 3.850 3.575 3.975 2.900 3.850 3.300
[61] 2.875 3.650 3.300 3.775 3.350 3.900 3.650 3.400 3.600 3.275 3.925 3.550
[73] 3.800 3.700 3.725
 [ reached getOption("max.print") -- omitted 75 entries ]

lapply(iris[, 1:4], mean)

$Sepal.Length
[1] 5.843333

$Sepal.Width
[1] 3.057333

$Petal.Length
[1] 3.758

$Petal.Width
[1] 1.199333

sapply(iris[, 1:4], mean)

Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
    5.843333     3.057333     3.758000     1.199333

tapply(iris[, 1], iris[, 5], mean)

    setosa versicolor  virginica 
     5.006      5.936      6.588

Exercices

Enoncé 1

Soit la fonction suivante :

Exo1 = function(M) {
    res = rep(0, 5)
    for (i in 1:5) {
        tmp = 0
        for (j in 1:4) {
            tmp = tmp + M[i, j]
        }
        res[i] = tmp
    }
    return(res)
}

M = matrix(1:20, nrow = 5, ncol = 4)
Exo1(M)

Proposer une fonction équivalente sans aucune boucle.

Enoncé 2

Réaliser une liste de $100$ réalisations d’une loi normale $\mathcal{N}(m,1)$ pour $m=-2$, $0$ et $2$ respectivement en utilisant lapply() et rnorm().
Créer un vecteur contenant la moyenne de chaque échantillon de la question 1.

Correction

Exercice 1 :

M = matrix(1:20, nrow = 5, ncol = 4)
apply(M, 1, sum)

[1] 34 38 42 46 50

Exercice 2 :

x = lapply(c(-2, 0, 2), function(x) {
    rnorm(1000, mean = x, sd = 1)
})
sapply(x, mean)

[1] -1.965681601 -0.005320404  2.041520544

Entrée / Sortie

Importation d’un jeu de données

Pour importer un tableau de données contenu dans un fichier texte en un data.frame, on utilise la fonction read.table(). Par exemple, pour un fichier nommé “Tableau.txt”, on utilisera la commande Tab1 = read.table("Tableau.txt") qui crée un data.frame Tab1. Si le fichier n’est pas placé dans le répertoire courant, on pourra spécifier le chemin d’accès de ce dernier directement dans la commande read.table(). Cette dernière admet les options principales suivantes :

header : indique si la première ligne contient des noms de variables. Par défaut, la valeur de cette option est FALSE.
sep : précise le séparateur de champ dans le fichier entre guillemets (” ” par défaut).
dec : le caractère utilisé pour les décimales (“.” par défaut).
row.names : indique par l’intermédiaire d’un vecteur de mode caractère le nom des lignes (par défaut : 1; 2; 3; : : : ).
col.names : idem pour les colonnes.
na.strings : précise la valeur des données manquantes. Par défaut, la valeur de cette option est “NA”.
nrows : nombre maximum de lignes à lire.
skip : nombre de lignes à sauter avant de commencer à lire des données. Cette option est utile quand le fichier texte contient par exemple un préambule.
blank.lines.skip : si “TRUE”, ignore les lignes blanches.
comment.char : précise le caractère utilisé pour faire des commentaires. Toutes les lignes commençant par ce caractère ne seront pas prises en compte.

Cette liste d’options n’est pas exhaustive (cf l’aide en ligne help(read.table)) mais permet déjà d’analyser un nombre conséquent de fichiers textes. Les fonctions read.csv() et read.csv2() en sont des cas particuliers, c’est-à-dire avec des options spécifiques (caractère séparateur, marque décimale) adaptées aux fichiers lus / écrits par des tableurs en format .csv .

Exercice

Enoncé

Executez les commandes suivantes pour préparer l’exercice.

data(iris)
dir.create("DataAux")
write.table(iris, file = "DataAux/iris1.txt", sep = ";", row.names = F, col.names = T)
rownames(iris) = paste("indiv", 1:nrow(iris), sep = "-")
write.table(iris, file = "DataAux/iris2.csv", row.names = T, col.names = F)
write.table(iris, file = "DataAux/iris3.txt", quote = FALSE, dec = ",", sep = "*")

Chargez à l’aide de la fonction read.table() les données iris1.txt, iris2.csv et iris3.txt disponibles dans le dossier DataAux.

Correction

iris1 = read.table("DataAux/iris1.txt", header = T, sep = ";")
head(iris1)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

iris2 = read.table("DataAux/iris2.csv", header = F, row.names = 1)
head(iris2)

         V2  V3  V4  V5     V6
indiv-1 5.1 3.5 1.4 0.2 setosa
indiv-2 4.9 3.0 1.4 0.2 setosa
indiv-3 4.7 3.2 1.3 0.2 setosa
indiv-4 4.6 3.1 1.5 0.2 setosa
indiv-5 5.0 3.6 1.4 0.2 setosa
indiv-6 5.4 3.9 1.7 0.4 setosa

iris3 = read.table("DataAux/iris3.txt", header = T, row.names = 1, sep = "*", dec = ",")
head(iris3)

        Sepal.Length Sepal.Width Petal.Length Petal.Width Species
indiv-1          5.1         3.5          1.4         0.2  setosa
indiv-2          4.9         3.0          1.4         0.2  setosa
indiv-3          4.7         3.2          1.3         0.2  setosa
indiv-4          4.6         3.1          1.5         0.2  setosa
indiv-5          5.0         3.6          1.4         0.2  setosa
indiv-6          5.4         3.9          1.7         0.4  setosa

Exportation

Exportation en fichier texte

Si maintenant on désire sauvegarder un objet R dans un fichier texte, on peut utiliser la commande write.table(). Les principales options de cette fonction sont :

file : nom du fichier dans lequel écrire (vérifier le répertoire courant)
append : prend une valeur logique. Si TRUE, R ajoute les données dans le fichier concerné sans effacer les précédentes. La valeur par défaut est FALSE.
sep : précise le séparateur à utiliser.
eol : caractère de fin de ligne. Par défaut prend la valeur “n” (retour chariot)
na : caractère à utiliser pour les données manquantes.
dec : précise le caractère à utiliser pour les décimales.

Sauvegarde `.RData`

R permet d’enregistrer des objets entiers, en conservant à la fois les données contenues dans les objets et les structures des objets.

La fonction save.image() peut être utilisée à tout moment pour enregistrer une image de session, c’est à dire l’ensemble des objets dans l’environnement de travail d’une session R. La sauvegarde d’une image de la session vous est également proposée lors de la fermeture de R.

save.image(file = "eximage.RData")

La fonction save() permet d’enregistrer spécifiquement un ou des objets dans un fichier de format .RData. Ce fichier peut être à tout moment rechargé sous R avec la fonction load(). Voici un exemple :

x <- stats::runif(20)
y <- list(a = 1, b = TRUE, c = "oops")
save(x, y, file = "xy.RData")
load("xy.RData")

On peut aussi enregistrer un seul objet, sans inclure le nom de l’objet, à l’aide de la fonction saveRDS(). L’objet, sauvegardé au format .rds peut être rechargé avec la fonction readRDS().

Pour plus de détails sur les importations et exportations, se référer au document R Data Import/Export disponible sur le CRAN.

Initiation au langage et objets de R