Chapitre 8 Analyse de covariance (ANCOVA)
Les slides associés à l’ANCOVA sont disponibles ici
Le jeu de données utilisé dans ce chapitre est disponible ici Ble.txt
8.1 Les données
Dans ce chapitre, nous allons présenter le modèle d’analyse de covariance (ANCOVA) seulement dans le cadre simple où on observe deux variables quantitatives \(z\) et \(Y\), et une variable qualitative \(T\) sur un échantillon de \(n\) individus : la variable quantitative \(Y\) est la variable réponse que l’on cherche à expliquer en fonction de la variable quantitative \(z\) (appelée ) et du facteur \(T\) à \(I\) niveaux. Les notions peuvent être généralisées pour plusieurs covariables et plusieurs facteurs.
Chaque individu de l’échantillon est repéré par un double indice \((i,j)\), \(i\) représente le niveau du facteur \(T\) auquel appartient l’individu et \(j\) correspond à l’indice de l’individu dans le niveau \(i\). Pour chaque individu \((i,j)\), on dispose d’une valeur \(z_{ij}\) de la variable \(z\) et d’une valeur \(Y_{ij}\) de la variable \(Y\). Pour chaque niveau \(i\) de \(T\) (avec \(i=1,\cdots, I\)), on observe \(n_i\) valeurs \(z_{(i)} =(z_{i1}, \cdots, z_{in_i})'\) de \(z\) et \(n_i\) valeurs \(Y_{(i)} = (Y_{i1}, \cdots, Y_{in_i})'\) de \(Y\). Au final \(n=\sum_{i=1}^I n_i\) est le nombre d’observations disponibles.
Dans tout ce chapitre, nous allons illustrer les notions abordées à l’aide de l’exemple suivant.
Example 8.1 On cherche à savoir si des conditions de température et d’oxygénation influencent l’évolution du poids des huîtres. On dispose de \(n = 20\) sacs de \(10\) huitres. On place, pendant un mois, ces \(20\) sacs de façon aléatoire dans \(I = 5\) emplacements différents d’un canal de refroidissement d’une centrale électrique à raison de \(n_i = 4\) sacs par emplacement. Ces emplacements se différencient par leurs températures et oxygénations. Pour chaque sac, on a
- son poids avant l’expérience (variable Pds Init),
- son poids après l’expérience (variable Pds Final),
- l’emplacement (variable Traitement) codé de 1 à 5.
InitWeight FinalWeight Treatment
1 27.2 32.6 1
2 32.0 36.6 1
3 33.0 37.7 1
4 26.8 31.0 1
5 28.6 33.8 2
6 26.8 31.7 2
7 26.5 30.7 2
8 26.8 30.4 2
9 28.6 35.2 3
10 22.4 29.1 3
11 23.2 28.9 3
12 24.4 30.2 3
13 29.3 35.0 4
14 21.8 27.0 4
15 30.3 36.4 4
16 24.3 30.5 4
17 20.4 24.6 5
18 19.6 23.4 5
19 25.1 30.3 5
20 18.1 21.8 5Les données peuvent être représentées conjointement sur un même graphique permettant de visualiser la relation éventuelle entre \(Y, \, z\) et \(T\). Il s’agit de tracer un nuage de points de coordonnées \((z_{ij},Y_{ij})\), où tous les points du niveau \(i\), \(i=1, \cdots, I\), sont représentés par le même symbole (Figure 8.1). On peut également tracer un boxplot du poids initial et du poids final pour chaque emplacement (Figure 8.2).
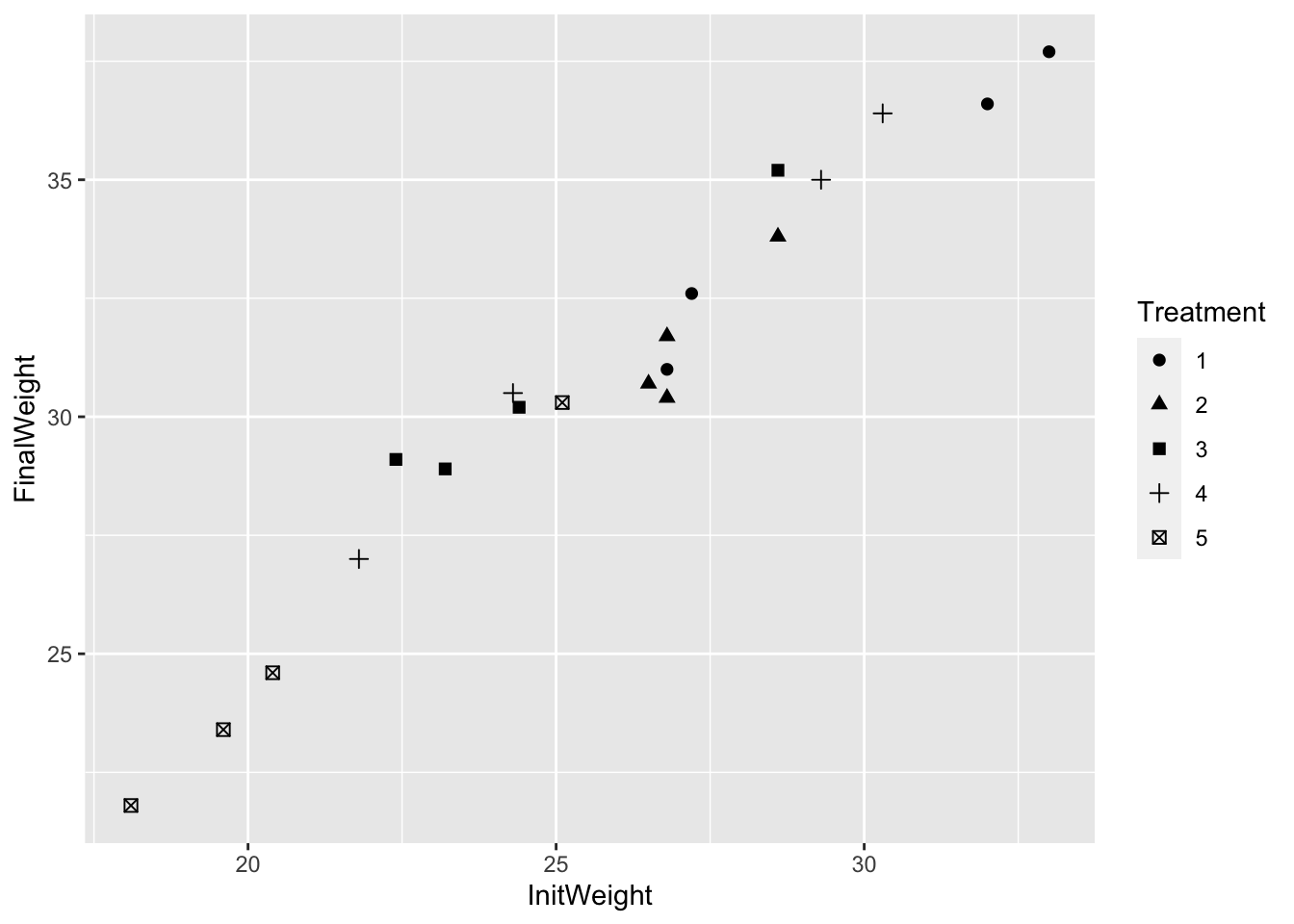
Figure 8.1: Graphique des poids finaux par rapport aux poids initiaux selon chaque emplacement.
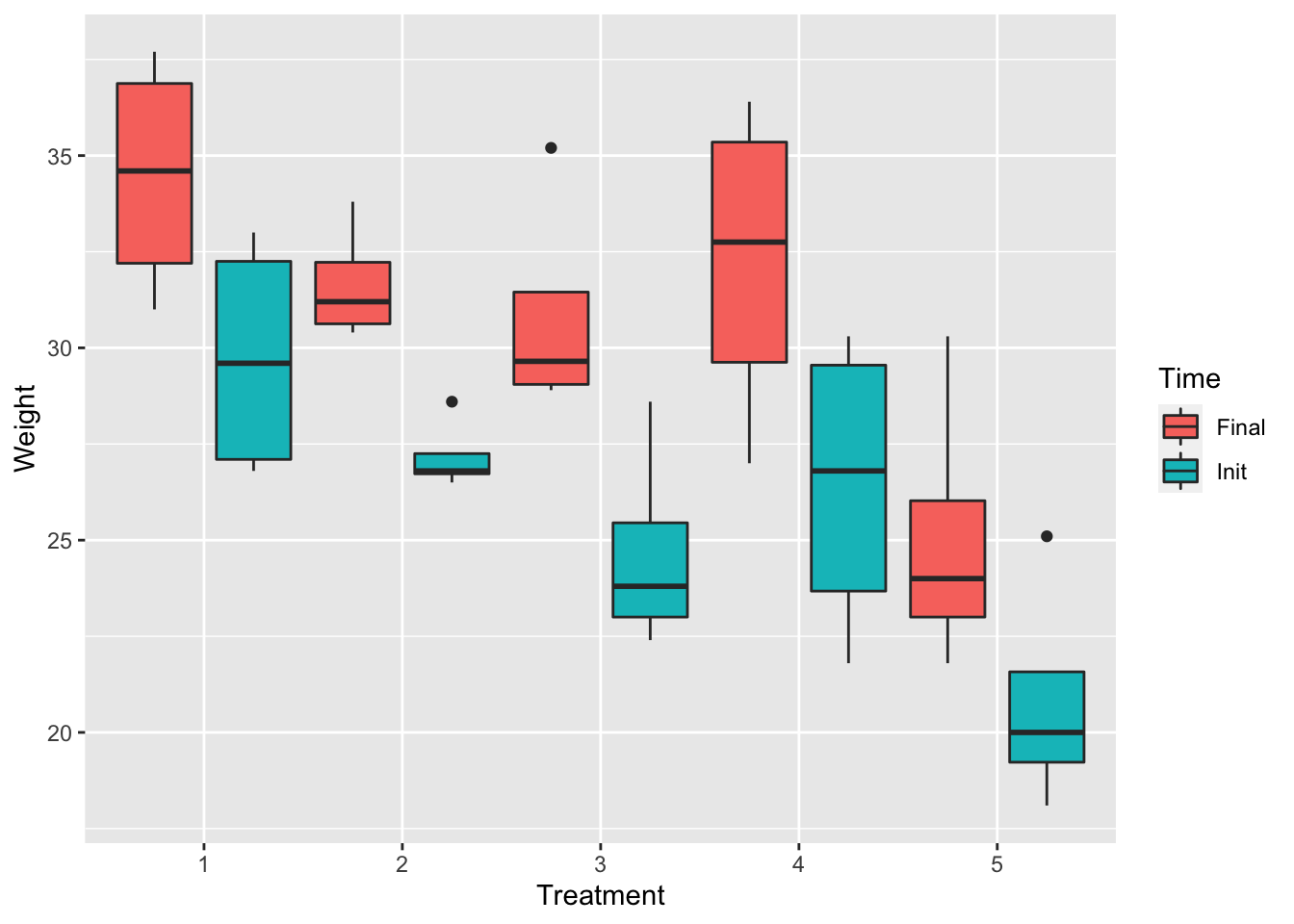
Figure 8.2: Evolution des poids initiaux et poids finaux pour chaque traitement
8.2 Modélisation
8.2.1 Modélisation régulière
Dans le cadre d’une ANCOVA simple, le modèle régulier s’écrit sous la forme : \[(MR) : Y_{ij} =a_i + b_i\ z_{ij} +\varepsilon_{ij}, \forall i=1, \cdots, I, \, j=1, \cdots, n_i\] où \(\varepsilon_{ij}\sim\mathcal{N}(0,\sigma^2)\), \(n\) variables indépendantes. Cela revient à estimer une droite de régression linéaire de \(Y\) sur \(z\) pour chaque niveau \(i\) du facteur \(T\). Pour le niveau \(i\), on estime les paramètres \(a_i\), constantes à l’origine des droites de régression et \(b_i\), pentes des droites de régression.
Matriciellement, le modèle s’écrit sous la forme \[ \underbrace{\left(\begin{array}{c} Y_{(1)} \\ \vdots \\ \vdots \\ Y_{(I)} \end{array}\right)}_{Y} = \underbrace{\left(\begin{array}{c c c c} X_{(1)} & & & \\ & X_{(2)} & & \\ & & \ddots & \\ & & & X_{(I)} \end{array}\right)}_{X} \underbrace{\left(\begin{array}{c} a_1 \\ b_1 \\ \vdots \\ a_I \\ b_I \end{array}\right)}_{\theta} + \underbrace{\left(\begin{array}{c} \varepsilon_{(1)} \\ \vdots \\ \vdots \\ \varepsilon_{(I)} \end{array}\right)}_{\varepsilon} \textrm{ avec } X_{(i)} = \left(\begin{array}{cc} 1& z_{i1}\\ \vdots&\vdots\\ 1& z_{i,n_i} \end{array}\right) \]
8.2.2 Modélisation singulière
Comme pour les modèles factoriels, il existe une reparamétrisation faisant apparaître des effets différentiels par rapport à un niveau de référence. Le modèle associé à cette nouvelle paramétrisation s’écrit :
\[ (MS) : Y_{ij} = (\mu + \alpha_i) + (\beta + \gamma_i) z_{ij} + \varepsilon_{ij},\ \ \forall i=1, \cdots, I, \, j=1, \cdots, n_i. \]
Cette paramétrisation permet de faire apparaître :
- un effet d’interaction entre la covariable \(z\) et le facteur \(T\) : \(\gamma_{i}\) ;
- un effet différentiel du facteur \(T\) sur la variable \(Y\) : \(\alpha_i\) ;
- un effet différentiel de la covariable \(z\) sur la variable \(Y\) : \(\beta\).
Exercise 8.1 Considérons le premier niveau comme référence dans cette paramétrisation (MS) pour rendre le modèle identifiable (ce qui est fait sous R par défaut). Les contraintes d’identifiabilité sont donc \(\alpha_1=\gamma_1=0\). Dans ce cas, donnez le lien entre les paramètres \(\mu\), \(\alpha_i\), \(\beta\), \(\gamma_i\) et les paramètres \(a_i\) et \(b_i\) de la modélisation (MR). Donnez une interprétation “graphique” des paramètres \(\mu\), \(\alpha_i\), \(\beta\) et \(\gamma_i\).
8.3 Estimation des paramètres
Dans le cas du modèle régulier (MR), on peut utiliser la formule générale \(\hat \theta = (X'X)^{-1}X'Y\). En utilisant le fait que la matrice \(X\) est diagonale par bloc, \(X=\mbox{diag}(X_{(1)},\ldots,X_{(I)})\), on obtient que
\[ \hat\theta = \left(\begin{array}{c} (X_{(1)}'X_{(1)})^{-1}X'_{(1)} Y_{(1)}\\ \vdots\\ X_{(I)}'X_{(I)})^{-1}X'_{(I)} Y_{(I)}\end{array}\right). \] On en déduit des résultats en régression linéaire simple que
\[ \left\{\begin{array}{l} \displaystyle \widehat{b}_i = \frac{\mbox{cov}(Y_{(i)},z_{(i)}) }{\mbox{var}(z_{(i)})} \\ \\ \widehat{a}_i = \bar Y_{(i)} - \bar z_{(i)} \widehat{b}_i \end{array}\right. \]
Dans notre exemple, on obtient les estimations suivantes :
a1 b1 a2 b2 a3 b3 a4 b4 a5 b5
1 5.241 0.983 -9.149 1.501 4.818 1.056 4.296 1.057 -0.432 1.224et on peut graphiquement observer l’ajustement des droites de régression aux données (Figure 8.3).
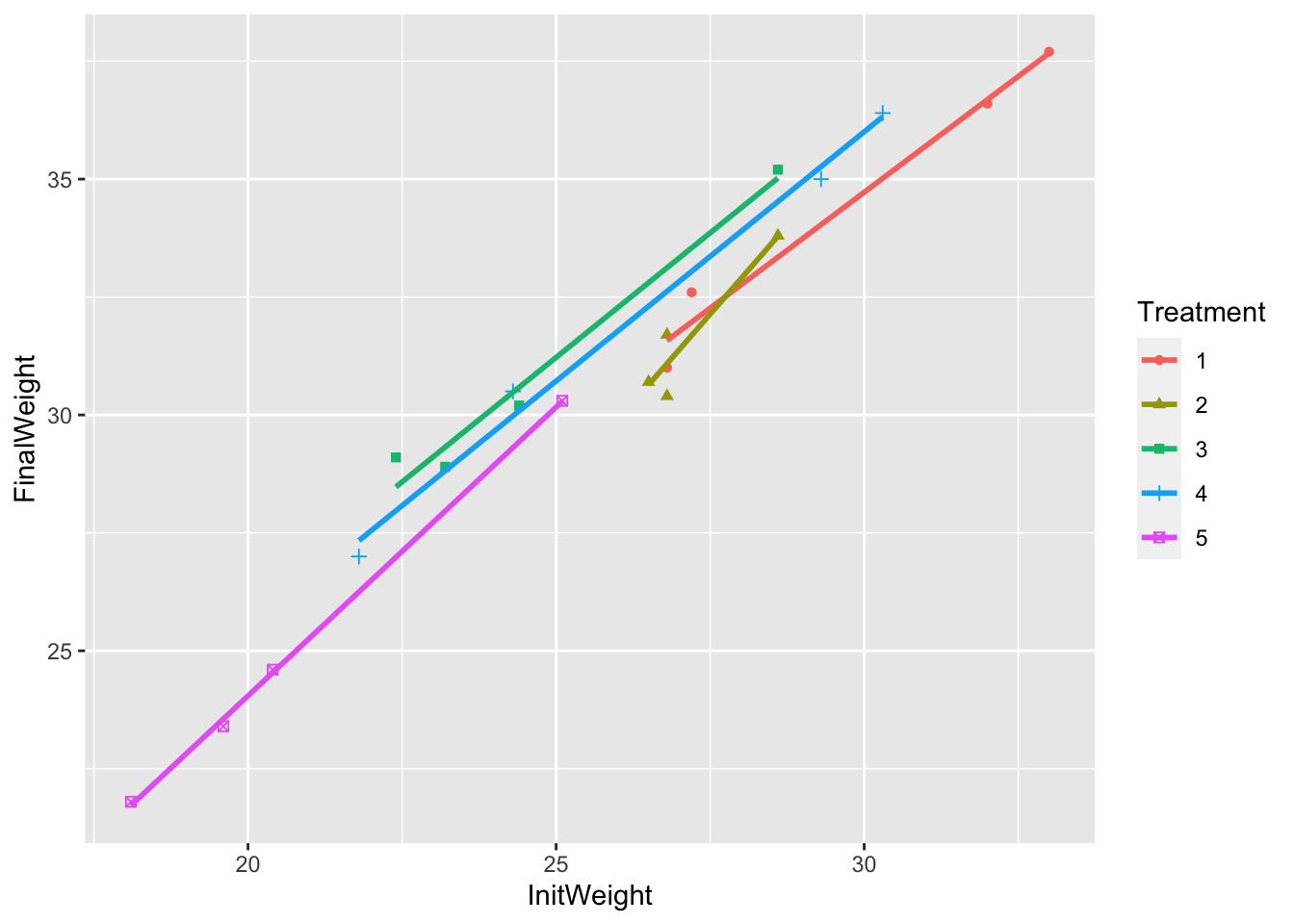
Figure 8.3: Ajustement des droites de régression aux données
Dans le cas du modèle singulier (MS) avec les contraintes d’identifiabilité \(\alpha_1=\gamma_1=0\), on peut déduire les estimateurs en faisant le lien entre de modèle singulier et le modèle régulier (MR). On obtient donc \[ \left\{ \begin{array}{l} \hat\mu = \hat a_1\\ \hat \alpha_i = \hat a_i - \hat a_1\\ \hat \beta = \hat b_1\\ \hat \gamma_i = \hat b_i - \hat b_1 \end{array} \right. \]
Dans notre exemple, on obtient les résultats suivants sous R
Call:
lm(formula = FinalWeight ~ InitWeight * Treatment, data = oyster)
Residuals:
Min 1Q Median 3Q Max
-0.68699 -0.28193 0.02184 0.10425 0.63075
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.24126 2.86473 1.830 0.0972 .
InitWeight 0.98265 0.09588 10.249 1.27e-06 ***
Treatment2 -14.39058 9.15971 -1.571 0.1472
Treatment3 -0.42330 3.97747 -0.106 0.9174
Treatment4 -0.94550 3.50725 -0.270 0.7930
Treatment5 -5.67309 3.57150 -1.588 0.1433
InitWeight:Treatment2 0.51871 0.33406 1.553 0.1515
InitWeight:Treatment3 0.07342 0.14699 0.499 0.6282
InitWeight:Treatment4 0.07428 0.12229 0.607 0.5571
InitWeight:Treatment5 0.24124 0.13980 1.726 0.1151
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5324 on 10 degrees of freedom
Multiple R-squared: 0.9921, Adjusted R-squared: 0.985
F-statistic: 139.5 on 9 and 10 DF, p-value: 2.572e-09On peut ensuite s’intéresser à construire des intervalles de confiance pour ces paramètres, faire des tests de nullité pour chacun des paramètres, …
8.4 Tests d’hypothèses
8.4.1 Absence de tout effet
On peut tout d’abord commencer par tester l’absence de tout effet, aussi bien de la covariable \(z\) que du facteur \(T\). Pour cela, on veut comparer le modèle “blanc” contre le modèle complet (MS)
\([M0] : Y_{ij} = \mu + \varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i\)
\([MS]: \ Y_{ij}=\mu + \alpha_i + \beta z_{ij} + \gamma_{i}z_{ij} +\varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i.\)
Le modèle \((M0)\) consiste à ajuster une droite horizontale aux données (Figure 8.4). Dans ce cas, la statistique de test du test de Fisher est
\[ F=\frac{SSE / (2I -1)}{SSR/n-2I} \underset{\mathcal{H}_0}{\sim} \mathcal{F}(2I-1,n-2I) \]
avec \(SSR=\|Y - \widehat{Y}\|^2\) et \(SSE=\|\widehat{Y} - \bar{Y}\mathbb{1}_n\|^2\).
Dans notre exemple, on obtient
Analysis of Variance Table
Model 1: FinalWeight ~ 1
Model 2: FinalWeight ~ InitWeight * Treatment
Res.Df RSS Df Sum of Sq F Pr(>F)
1 19 358.67
2 10 2.83 9 355.84 139.51 2.572e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1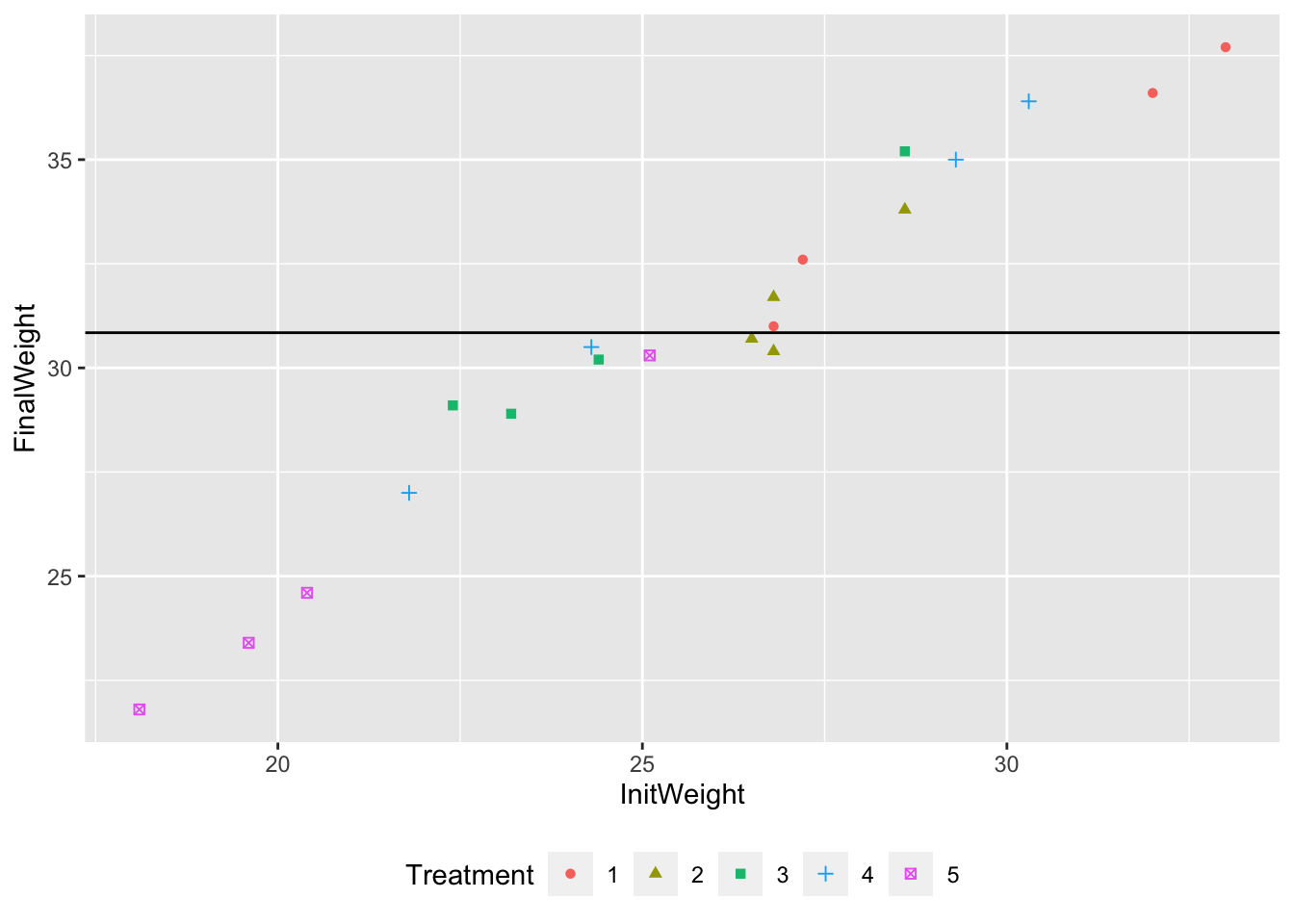
Figure 8.4: Ajustement du modèle (M0) aux données.
Si on rejette le modèle (M0), on peut poursuivre l’étude mais il est important de suivre une démarche logique dans la mise en place des tests d’hypothèses, comme dans le cadre de l’analyse de la variance.
8.4.2 Test d’absence d’interaction
On commence par tester l’hypothèse de non-interaction entre le facteur \(T\) et la covariable \(z\). On souhaite donc tester l’hypothèse nulle suivante :
\[ \mathcal{H}_0^{(MnonI)} : b_1= b_2 = \cdots = b_I \Longleftrightarrow \gamma_{1} = \gamma_{2} = \cdots = \gamma_{I} = 0. \]
Ce test revient à comparer le modèle complet et le sous-modèle sans interaction :
\([MS]: \ Y_{ij}=\mu + \alpha_i + (\beta+ \gamma_{i}) z_{ij} +\varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i\)
\([MnonI]:\ Y_{ij}=\mu + \alpha_i+ \beta z_{ij} +\varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i.\)
Le modèle \([MnonI]\) consiste graphiquement à ajuster des droites parallèles pour chaque traitement (Figure 8.5).
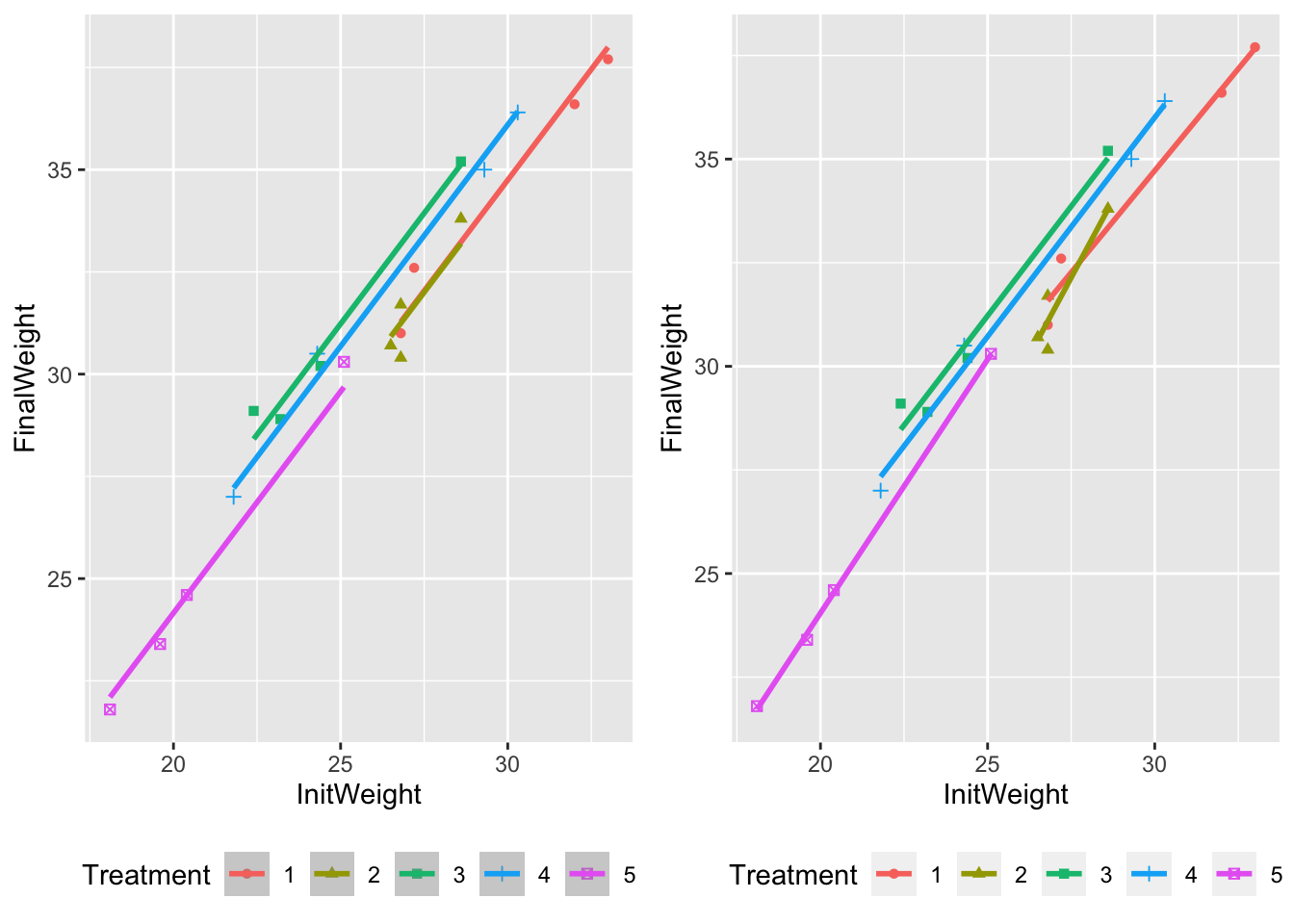
Figure 8.5: Ajustement du modèle d’ANCOVA sans interaction (à gauche) et avec interaction (à droite).
La statistique de test de Fisher vaut dans ce cas
\[ F = \frac{SSR_{nonI}-SSR / (I-1)}{SSR/(n-2I)}\underset{\mathcal{H}_0}{\sim}\mathcal{F}(I-1,n-2I) \]
Si on rejette l’hypothèse \(\mathcal{H}_0^{[MnonI]}\), on conclut à la présence d’interactions dans le modèle. Il est alors inutile de tester l’absence d’effet du facteur \(T\) ou de la covariable \(z\) sur \(Y\), car toute variable constituant une interaction doit apparaître dans le modèle. En revanche, si le test montre que l’hypothèse \(\mathcal{H}_0^{[MnonI]}\) est vraisemblable (i.e. les \(I\) droites de régression partagent la même pente de régression), on peut alors évaluer l’effet de la covariable \(z\) sur \(Y\) et celui du facteur \(T\) sur \(Y\).
Dans notre exemple, on retient le modèle sans interaction. Nous allons donc poursuivre notre étude.
Call:
lm(formula = FinalWeight ~ InitWeight + Treatment)
Residuals:
Min 1Q Median 3Q Max
-0.8438 -0.3154 -0.2171 0.4863 0.8871
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.25040 1.44308 1.559 0.141205
InitWeight 1.08318 0.04762 22.746 1.87e-12 ***
Treatment2 -0.03581 0.40723 -0.088 0.931169
Treatment3 1.89922 0.45802 4.147 0.000988 ***
Treatment4 1.35157 0.41937 3.223 0.006135 **
Treatment5 0.24446 0.57658 0.424 0.678022
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5492 on 14 degrees of freedom
Multiple R-squared: 0.9882, Adjusted R-squared: 0.984
F-statistic: 235 on 5 and 14 DF, p-value: 5.493e-13Analysis of Variance Table
Model 1: FinalWeight ~ InitWeight + Treatment
Model 2: FinalWeight ~ InitWeight * Treatment
Res.Df RSS Df Sum of Sq F Pr(>F)
1 14 4.2223
2 10 2.8340 4 1.3883 1.2247 0.36028.4.3 Test d’absence de l’effet de la covariable z
On souhaite tester l’hypothèse d’absence d’effet de la covariable \(z\) sur \(Y\) : \[\mathcal{H}_0^{[MT]} : b_1= b_2= \cdots = b_I= 0.\] Seul le facteur \(T\) explique \(Y\). On met donc en place un modèle d’analyse de la variance à un facteur (Figure 8.6).
On est donc ramené à comparer le modèle d’ANCOVA sans interaction avec le modèle d’anova à un facteur \[[MT]: \ Y_{ij}=\mu + \alpha_i +\varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i.\]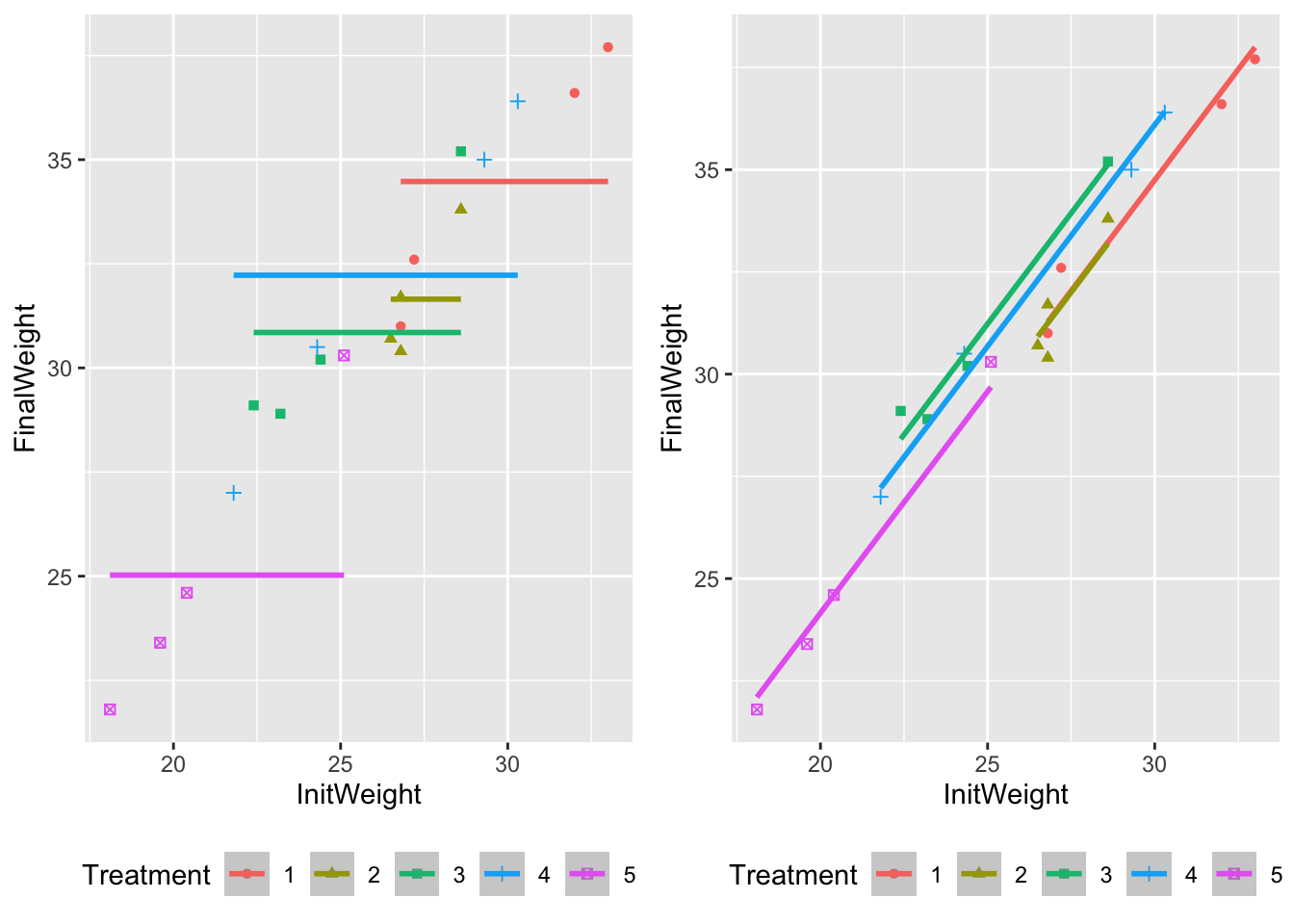
Figure 8.6: Ajustement du modèle d’analyse de la variance à un facteur (à gauche) et le modèle d’ANCOVA sans interaction (à droite).
La statistique de test de Fisher s’exprime alors comme suit : \[ F=\frac{SSR_T - SSR_{nonI} / 1}{SSR_{nonI}/(n-(I+1))}\underset{\mathcal{H}_0}{\sim}\mathcal{F}(1,n-(I+1)) \]
Dans notre exemple, on rejette l’absence d’effet du poids initial au risque \(5\%\).
Analysis of Variance Table
Model 1: FinalWeight ~ Treatment
Model 2: FinalWeight ~ InitWeight + Treatment
Res.Df RSS Df Sum of Sq F Pr(>F)
1 15 160.263
2 14 4.222 1 156.04 517.38 1.867e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 18.4.4 Test d’absence de l’effet facteur T
On veut tester l’hypothèse d’absence d’effet du facteur \(T\) sur \(Y\)
\[\mathcal{H}_0^{[Mz]} : a_1=a_2=\ldots=a_I \Longleftrightarrow \alpha_1= \alpha_2 = \ldots = \alpha_I = 0.\]
Les \(I\) droites de régression partagent la même constante à l’origine, seule la covariable \(z\) explique \(Y\). On met alors en place un modèle de régression linéaire simple (Figure 8.7)
On est donc ramené à comparer le modèle d’ANCOVA sans interaction avec un modèle de régression linéaire simple
\[[Mz]:\ Y_{ij}=\mu + \beta\ z_{ij} +\varepsilon_{ij},\, \forall i=1, \cdots, I,\, \forall j=1, \cdots, n_i\]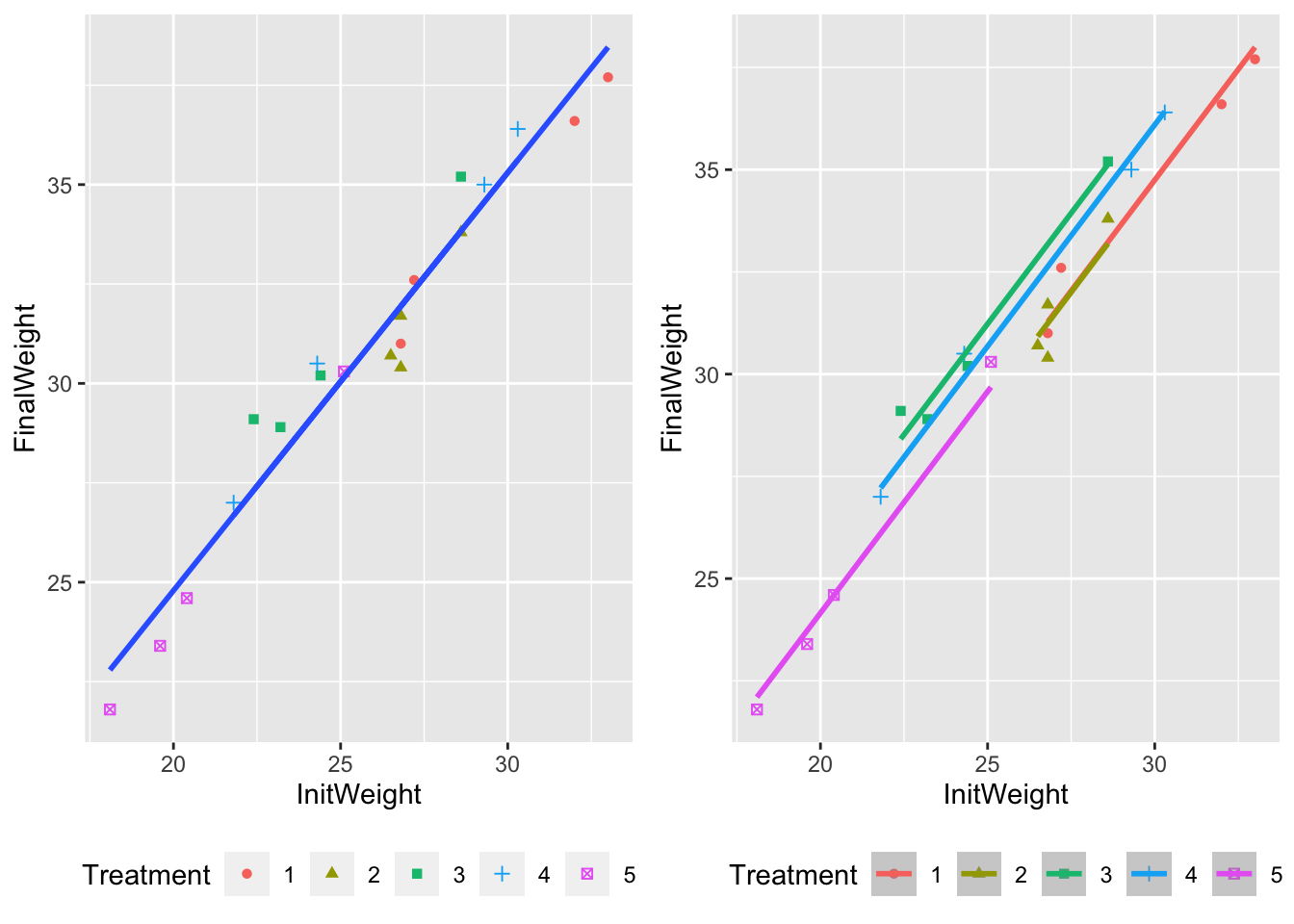
Figure 8.7: Ajustement du modèle de régression linéaire simple (à gauche) et du modèle d’ANCOVA sans interaction (à droite).
Dans ce cas, la statitsique de test de Fisher est définie par
\[ F=\frac{SSR_z - SSR_{nonI} / (I-1)}{SSR_{nonI} / (n-(I+1))}\underset{\mathcal{H}_0}{\sim}\mathcal{F}(I-1,n-(I+1)) \]
Pour notre exemple, on rejette également l’absence d’effet du traitement.
Analysis of Variance Table
Model 1: FinalWeight ~ InitWeight
Model 2: FinalWeight ~ InitWeight + Treatment
Res.Df RSS Df Sum of Sq F Pr(>F)
1 18 16.3117
2 14 4.2223 4 12.089 10.021 0.0004819 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 18.5 En résumé
- Savoir écrire un modèle d’ANCOVA (individuellement et matriciellement), régulier et singulier
- Savoir distinguer un modèle régulier d’un modèle singulier
- Savoir estimer les paramètres du modèle d’ANCOVA dans le cas régulier et dans le cas singulier (en s’adaptant à la / les contrainte(s) choisie(s))
- Savoir construire un intervalle de confiance pour un paramètre du modèle d’ANCOVA
- Savoir construire un test pour tester l’effet du facteur, l’effet d’interaction, … et savoir organiser ces différents tests
- Savoir associer une représentation graphique à un sous-modèle d’ANCOVA
8.6 Quelques codes en python
import statsmodels.api as sm
from statsmodels.formula.api import ols
# Récupération des données
oysterpy=r.oyster;
# Ajustement du modèle d'ANCOVA avec inetraction
completpy = ols('FinalWeight ~ InitWeight * Treatment', data=oysterpy).fit();
completpy.summary()<class 'statsmodels.iolib.summary.Summary'>
"""
OLS Regression Results
==============================================================================
Dep. Variable: FinalWeight R-squared: 0.992
Model: OLS Adj. R-squared: 0.985
Method: Least Squares F-statistic: 139.5
Date: Jeu, 28 oct 2021 Prob (F-statistic): 2.57e-09
Time: 12:20:28 Log-Likelihood: -8.8384
No. Observations: 20 AIC: 37.68
Df Residuals: 10 BIC: 47.63
Df Model: 9
Covariance Type: nonrobust
=============================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------------
Intercept 5.2413 2.865 1.830 0.097 -1.142 11.624
Treatment[T.2] -14.3906 9.160 -1.571 0.147 -34.800 6.019
Treatment[T.3] -0.4233 3.977 -0.106 0.917 -9.286 8.439
Treatment[T.4] -0.9455 3.507 -0.270 0.793 -8.760 6.869
Treatment[T.5] -5.6731 3.572 -1.588 0.143 -13.631 2.285
InitWeight 0.9826 0.096 10.249 0.000 0.769 1.196
InitWeight:Treatment[T.2] 0.5187 0.334 1.553 0.152 -0.226 1.263
InitWeight:Treatment[T.3] 0.0734 0.147 0.499 0.628 -0.254 0.401
InitWeight:Treatment[T.4] 0.0743 0.122 0.607 0.557 -0.198 0.347
InitWeight:Treatment[T.5] 0.2412 0.140 1.726 0.115 -0.070 0.553
==============================================================================
Omnibus: 0.296 Durbin-Watson: 1.831
Prob(Omnibus): 0.862 Jarque-Bera (JB): 0.466
Skew: 0.158 Prob(JB): 0.792
Kurtosis: 2.321 Cond. No. 2.22e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.22e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
"""# Test d'absence de tout effet
from statsmodels.stats.anova import anova_lm
M0py = ols('FinalWeight~1', data=oysterpy).fit()
anova_lm(M0py,completpy) df_resid ssr df_diff ss_diff F Pr(>F)
0 19.0 358.669500 0.0 NaN NaN NaN
1 10.0 2.834009 9.0 355.835491 139.510053 2.572066e-09# Test d'absence d'interaction
nonIpy = ols('FinalWeight ~ InitWeight + Treatment', data=oysterpy).fit()
from statsmodels.stats.anova import anova_lm
anova_lm(nonIpy,completpy) df_resid ssr df_diff ss_diff F Pr(>F)
0 14.0 4.222323 0.0 NaN NaN NaN
1 10.0 2.834009 4.0 1.388314 1.224691 0.360175# Test d'absence de l'effet de la covariable
MTpy = ols('FinalWeight ~ Treatment', data=oysterpy).fit()
anova_lm(MTpy,nonIpy) df_resid ssr df_diff ss_diff F Pr(>F)
0 15.0 160.262500 0.0 NaN NaN NaN
1 14.0 4.222323 1.0 156.040177 517.383995 1.867369e-12# Test d'absence de l'effet du facteur
Mzpy = ols('FinalWeight ~ InitWeight', data=oysterpy).fit()
anova_lm(Mzpy,nonIpy) df_resid ssr df_diff ss_diff F Pr(>F)
0 18.0 16.311683 0.0 NaN NaN NaN
1 14.0 4.222323 4.0 12.089359 10.021203 0.000482