Chapitre 9 Principe du modèle linéaire généralisé

Les slides associés à ce chapitre sont disponibles ici

9.1 Introduction

Nous observons un vecteur \(Y\) de taille \(n\), réalisation d’une variable aléatoire de moyenne \(\mu\) et dont les composants sont indépendants. Dans le cadre du modèle linéaire, on a \(\mu = X\theta\) où \(X\) est une matrice \(n\times k\): le design. Le vecteur \(\theta\) est inconnu et modélise l’influence des variables explicatives sur la réponse \(Y\).

Le modèle linéaire tel que nous l’avons vu dans la partie précédente peut donc être caractérisé de la manière suivante :

1. une composante aléatoire : \(Y\) est un vecteur aléatoire gaussien de moyenne \(\mu\) (\(Y\sim\mathcal{N}_n(\mu,\sigma^2 I_n)\)),
2. une composante “systématique” : les variables explicatives \(\textbf{x}^{(1)}, \cdots, \textbf{x}^{(p)}\) définissent un prédicteur linéaire \(\eta=X\theta\) avec \(\theta\in\mathbb{R}^k\) (\(k\) est lié à \(p\))
3. la relation liant \(\mu\) et \(\eta\) : \(\mu=\eta\) pour le modèle linéaire.

Imposer une dépendance linéaire entre les variables explicatives et \(\mathbb{E}[Y]\) permet une étude approfondie mais peut être parfois trop restrictive. Une généralisation possible du modèle linéaire consiste donc à supposer que la relation liant \(\mu\) à \(\eta\) n’est pas l’identité, mais plutôt un lien du type: \[\eta_i = g(\mu_i), \ \mathrm{pour} \ \eta=(\eta_1,\dots,\eta_n)' \ \mathrm{et} \ \mu=(\mu_1,\dots, \mu_n)'.\] La fonction \(g\) modélise donc le lien entre ces deux vecteurs. Cette formulation permet de modéliser un panel plus riche d’expériences.

Example 9.1 Dans une expérience clinique, on cherche à comparer deux modes opératoires pour une opération chirurgicale donnée. L’expérience est menée sur deux hôpitaux différents. On dispose donc ici de deux facteurs à deux modalités: et hôpital. La variable réponse correspond pour chaque patient au succès ou à l’échec de l’intervention : il s’agit d’une variable binaire.

Example 9.2 Un assureur s’intéresse au nombre de sinistres automobile déclarés pendant ces dix dernières années. Il souhaite étudier si ce nombre de sinistres est lié à l’âge du conducteur, la taille de la voiture, …. Le nombre de sinistres peut être modélisé par une loi de Poisson.

Dans le cas particulier où la fonction de lien est de type canonique (i.e. \(g(x)=x\)), rien n’interdit d’utiliser la méthode des moindres carrés introduite dans la partie précédente. Cette dernière est en effet purement géométrique et peut donc tout à fait s’appliquer à des réponses de type “binaire”. Cependant, la partie inférentielle traitée dans ce cours nécessite quant à elle des hypothèses très fortes sur la distribution des observations. Pour des modèles alternatifs, il faut donc complètement repenser la construction des tests et des intervalles de confiance. Par ailleurs, une relation de type canonique est relativement restrictive (cf Figure 9.1). Il convient donc de se placer dans un cadre plus général afin de pouvoir faire face à des problèmes plus variés.

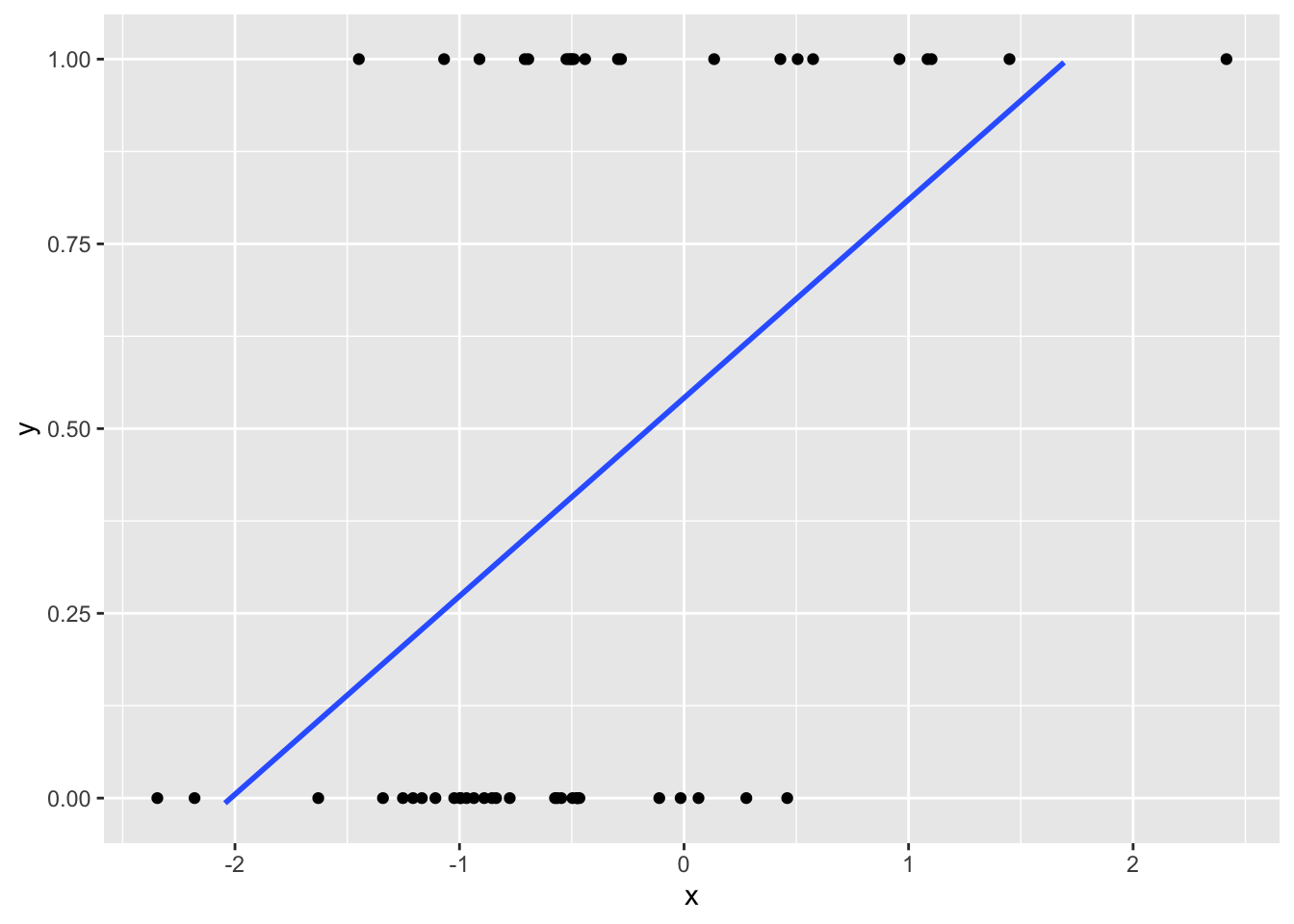
Figure 9.1: Exemple d’observations pour un modèle de type binaire

De manière plus générale, la méthode des moindres carrés introduite dans la partie précédente ne peut être implémentée. Bien souvent, le problème d’optimisation associé n’est en effet pas convexe. Une première “parade” consiste à utiliser l’estimateur du maximum de vraisemblance… mais dans la plupart des cas, ce dernier n’est pas calculable analytiquement. Il est cependant possible d’utiliser un algorithme itératif inspiré de la méthode de Newton-Raphson permettant d’approcher le maximum de vraisemblance. Sous certaines conditions, cet algorithme propose des résultats tout à fait satisfaisants.

9.2 Caractérisation d’un modèle linéaire généralisé

L’objet de cette section est d’introduire le cadre théorique global permettant de regrouper tous les modèles (linéaire gaussien, logistique, log-linéaire) de ce cours qui cherchent à modéliser l’espérance d’une variable réponse \(Y\) en fonction d’une combinaison linéaire de variables explicatives. Le modèle linéaire généralisé développé initialement en 1972 par Nelder et Wedderburn et dont on trouvera des exposés détaillés dans McCullagh (2018), Agresti (2003) ou Antoniadis, Berruyer, and Carmona (1992), n’est ici qu’esquissé afin de définir les concepts communs à ces modèles : famille exponentielle, estimation par maximum de vraisemblance, tests, …

Le modèle linéaire généralisé est caractérisé par trois quantités :

1. La variable réponse \(Y\), composante aléatoire à laquelle est associée une loi de probabilité
2. les variables explicatives \(\textbf{x}^{(1)},\ldots,\textbf{x}^{(p)}\) (prédicteurs)
3. le lien qui décrit la relation fonctionnelle entre la combinaison linéaire des \(\textbf{x}^{(1)},\ldots,\textbf{x}^{(p)}\) et l’espérance de la variable réponse \(Y\).

Nous allons par la suite détailler ces différentes quantités.

9.2.1 Loi de la variable réponse \(Y\)

La composante aléatoire identifie la distribution de probabilité de la variable à expliquer \(Y\). On suppose que l’échantillon statistique est constitué de \(n\) variables aléatoires \((Y_i)_{i=1,\cdots, n}\) indépendantes admettant des distributions issues d’une structure de famille exponentielle.

Definition 9.1 Soit \(Y\) une variable aléatoire unidimensionnelle. On dit que la loi de \(Y\) appartient à une famille exponentielle si la loi de \(Y\) est dominée par une mesure dite de référence et si la vraisemblance de \(Y\) calculée en \(y\) par rapport à cette mesure s’écrit de la façon suivante : \[\begin{equation} f_Y(y,\omega,\phi) = \exp \left[ \frac{y \omega -b(\omega)}{\gamma(\phi)}+c(y,\phi) \right]. \tag{9.1} \end{equation}\] Le paramètre \(\omega\) est appelé le paramètre naturel de la famille exponentielle.

Cette formulation inclut la plupart des lois usuelles comportant un ou deux paramètres : gaussienne, gaussienne inverse, gamma, Poisson, binomiale (cf Table ??). Attention, la mesure de référence change d’une structure exponentielle à l’autre : la mesure de Lebesgue pour une loi continue, une mesure discrète combinaison de Dirac pour une loi discrète. Consulter Antoniadis, Berruyer, and Carmona (1992) pour une présentation générale de la famille exponentielle et des propriétés asymptotiques des estimateurs de leurs paramètres.

Proposition 9.1 Soit \(Y\) une variable aléatoire dont la loi de probabilité appartient à la famille exponentielle alors \[ \mathbb{E}[Y]=b'(\omega) \textrm{ et } \mbox{Var}(Y)=b''(\omega)\gamma(\phi). \]

Exercise 9.1 Pour démontrer cette proposition,

• pour évaluer \(\mathbb{E}[Y]\) : calculer \(\frac{\partial }{\partial \omega} f_{Y}(y,\omega,\phi)\) et intégrer par rapport à \(y\)
• pour évaluer \(\mbox{Var}(Y)\) : calculer \(\frac{\partial^2 }{\partial \omega^2} f_{Y}(y,\omega,\phi)\) et intégrer par rapport à \(y\)

Pour certaines lois, la fonction \(\gamma\) est de la forme : \(\gamma(\phi)=\phi\). Dans ce cas, \(\phi\) est appelé paramètre de dispersion, c’est un paramètre de nuisance intervenant par exemple lorsque les variances des lois gaussiennes sont inconnues, mais égal à 1 pour les lois à un paramètre (Poisson, Bernoulli). L’expression de la structure exponentielle se met alors sous la forme canonique : \[\begin{equation} \tag{9.2} f(y,\omega)=a(\omega)d(y)\exp[yQ(\omega)] \end{equation}\] avec \(Q(\omega)= \frac{\omega}{\phi}\), \(a(\omega) = \exp\left(-\frac{b(\omega)}{\phi}\right)\) et \(d(y)= \exp[c(y,\phi)]\).

Example 9.3 Exemples dans la famille exponentielle :

• Loi gaussienne : La densité de la loi \(\mathcal{N}(\mu,\sigma^2)\) s’écrit : \[\begin{eqnarray*} f(y, \mu,\sigma^2)&=&\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(y-\mu)^2}{2\sigma^2}\right\}\\ &=& \exp\left[\frac{y \mu - \mu^2 /2}{\sigma^2} - \left(\frac{1}{2}\frac{y^2}{\sigma^2} + \frac{1}{2}\ln(2\pi\sigma^2) \right)\right] \\ &=&\exp\left\{-\frac{1}{2}\frac{\mu^2}{\sigma^2}\right\}\exp\left\{-\frac{1}{2}\frac{y^2}{\sigma^2}-\frac{1}{2}\ln(2\pi\sigma^2) \right\}\exp\left\{y\frac{\mu}{\sigma^2} \right\}. \end{eqnarray*}\]

La famille gaussienne est une famille exponentielle de paramètre de dispersion \(\phi=\sigma^2\) et de paramètre naturel \(\omega=\mathbb{E}[Y]=\mu\).

• Loi de Bernoulli : Soit \(Y\) une variable aléatoire de loi de Bernoulli \(\mathcal B(\pi)\), alors \[ f(y, \pi)=\pi^{y}(1-\pi)^{1-y}=(1-\pi)\exp\left\{y\ln\frac{\pi}{1-\pi}\right\}, \] qui est la forme d’une structure exponentielle de paramètre naturel \(\omega=\ln(\frac{\pi}{1-\pi}).\)

La loi binomiale conduit à des résultats identiques en considérant la somme de \(n\) (connu) variables de Bernoulli.

• Loi de Poisson : On considère une variable \(Y\) de loi de Poisson de paramètre \(\lambda\). Alors \[ f(y, \lambda)=\frac{\lambda^{y}e^{-\lambda}}{y!}=\exp\left\{-\lambda\right\}\frac{1}{y!}\exp\left\{y \ln\lambda\right\} = \exp\left [y \ln(\lambda)-\lambda - \ln(y!)\right] \] qui est issue d’une structure exponentielle et, mise sous la forme canonique, de paramètre naturel \(\omega=\ln(\lambda)\).

Distribution	\(\omega\)	\(b(\omega)\)	\(\gamma(\phi)\)	\(\mathbb{E}[Y]=b'(\omega)\)	\(\mbox{Var}(Y)=b^{''}(\omega)\gamma(\phi)\)
Gaussienne \(\mathcal N(\mu,\sigma^2)\)	\(\mu\)	\(\frac{\omega^2}{2}\)	\(\phi = \sigma^2\)	\(\mu=\omega\)	\(\sigma^2\)
Bernoulli \(\mathcal B(p)\)	\(\ln(p/1-p)\)	\(\ln(1+e^\omega)\)	\(1\)	\(p=\frac{e^\omega}{1+e^\omega}\)	\(p(1-p)\)
Poisson \(\mathcal P(\lambda)\)	\(\ln(\lambda)\)	\(\lambda=e^{\omega}\)	\(1\)	\(\lambda=e^{\omega}\)	\(\lambda=e^{\omega}\)
Gamma \(\mathcal G(\mu,\nu)\)	\(-\frac{1}{\mu}\)	\(-\ln(-\omega)\)	\(\frac{1}{\nu}\)	\(\mu=-\frac{1}{\omega}\)	\(\frac{\mu^2}{\nu}\)
Inverse Gaussienne \(IG(\mu,\sigma^2)\)	\(-\frac{1}{2\mu^2}\)	\(-\sqrt{-2\omega}\)	\(\sigma^2\)	\(\mu=(\sqrt{-2\omega})^{-1}\)	\(\mu^3 \sigma^2\)

9.2.2 Prédicteur linéaire

Les observations planifiées des variables explicatives sont organisées dans la matrice \(\mathbf{X}\) de planification d’expérience (design matrix). Soit \(\theta\) un vecteur de \(k\) (\(=p+1\)) paramètres. Le prédicteur linéaire, composante déterministe du modèle est le vecteur à \(n\) composantes défini par \[\eta = \mathbf{X}\theta.\]

9.2.3 Fonction de lien

Cette troisième quantité exprime une relation fonctionnelle entre la composante aléatoire et le prédicteur linéaire. Soit \(\mu_i=\mathbb{E}[Y_i] \, ; \, i=1,\cdots,n\). On pose \[\forall i=1,\cdots,n, \, \eta_i=g(\mu_i)\] où \(g\), appelée fonction de lien, est supposée monotone et différentiable. Ceci revient donc à écrire un modèle dans lequel une fonction de la moyenne appartient au sous-espace vectoriel engendré par les variables explicatives : \[\forall i=1,\cdots, n, \, g(\mu_i)=\mathbf{x}_i\theta.\] La fonction de lien qui associe la moyenne \(\mu_i\) au paramètre naturel \(\omega_i\) est appelée fonction de lien canonique. Dans ce cas, \[\forall i=1,\cdots, n, \, g(\mu_i)=\omega_i=\mathbf{x}_i\theta.\]

Example 9.4 La fonction de lien canonique pour

• la loi gaussienne est l’identité : \(\omega_i = \mu_i\)
• la loi de Poisson est le logarithme \(\omega_i = \ln(\mu_i)\)
• la loi de Bernoulli est la fonction logit \(\omega_i = \ln\left(\frac{\mu_i}{1-\mu_i}\right)\)

Dans le cas d’une variable réponse binaire \(Y\), on peut aussi considérer la fonction de lien probit : \[ \eta_i = g(\pi_i) = \Phi^{-1}(\pi_i) \] où \(\Phi(.)\) est la fonction de répartition de la loi normale \(\mathcal N(0,1)\).

Dans le cadre de l’étude d’une variable réponse \(Y\) suivant une loi binomiale et considérant la fonction de lien logit, le modèle linéaire généralisé est appelé régression logistique. Dans le cadre de l’étude d’une variable réponse \(Y\) suivant une loi de Poisson et considérant la fonction de lien logarithme, le modèle linéaire généralisé est appelé modèle log-linéaire.

9.3 Estimation

Le modèle étant posé, on souhaite maintenant estimer le vecteur des paramètres \(\theta=(\theta_1,\ldots,\theta_k)'\) et le paramètre de dispersion \(\phi\). Comme ce dernier paramètre n’apparait pas dans l’espérance, ce n’est pas le paramètre d’intérêt. Pour simplifier, on va supposer par la suite que \(\phi\) est fixé (ou estimé préalablement), seul \(\theta\) reste à estimer.

9.3.1 Estimation par maximum de vraisemblance

La méthode des moindres carrés n’est pas applicable dans un grand nombre de situations pour le modèle linéaire généralisé (excepté pour des fonctions de lien canonique, i.e. identité). Pour ce problème d’estimation, on utilise donc la méthode d’estimation du maximum de vraisemblance (EMV). On va donc maximiser la log-vraisemblance du modèle linéaire généralisé.

Par indépendance des observations, la vraisemblance du n-échantillon \(\underline{Y}=(Y_1,\ldots,Y_n)\) s’écrit \(\theta\mapsto L(\underline{Y};\theta)\) telle que \[\theta \mapsto L(\underline{y}; \theta) = \prod_{i=1}^n f_{Y_i}(y_i; \omega_i)\] et la log-vraisemblance vaut \(\theta\mapsto l(Y;\theta)\) avec \[\theta\mapsto l(\underline{y}; \theta) = \sum_{i=1}^n \ln[f_{Y_i}(y_i; \omega_i)],\] où \(\theta\), \(\eta\), \(\mu\) et \(\omega\) sont liés par le modèle. L’EMV associé vérifie donc \[\widehat{\theta}_{\scriptsize MV} \in \mathrm{arg} \max_{\theta} L(\underline{Y}; \theta) = \mathrm{arg} \max_{\theta} l(\underline{Y}; \theta).\] En particulier, si la fonction de lien \(g\) est celle du lien canonique, on a \(\omega_i=\textbf{x}_i \theta\) et donc \[l(\underline{y}; \theta) = \sum_{i=1}^n \frac{y_i \textbf{x}_i \theta -b(\textbf{x}_i \theta)}{\gamma(\phi)}+c(y_i,\phi).\]

Afin d’obtenir une expression de l’EMV, on s’intéresse au score \[S(\underline{Y};\theta) = \left( \frac{\partial}{\partial \theta_1} l(\underline{Y};\theta), \dots , \frac{\partial}{\partial \theta_k} l(\underline{Y}; \theta)\right)'.\] L’estimateur du maximum de vraisemblance vérifie donc \[\begin{equation} S(\underline{Y};\widehat{\theta}_{\scriptsize MV})=0_k. \tag{9.3} \end{equation}\] Dans le cas particulier où \(g\) est le lien canonique, on a \[ \forall j=1,\ldots,k,\ \frac{\partial}{\partial \theta_j} l(\underline{y};\theta) = \sum_{i=1}^n \frac{1}{\gamma(\phi)} x_i^{(j)} [y_i - b'(\textbf{x}_i \theta)] = 0 \Leftrightarrow \sum_{i=1}^n [y_i - b'(\textbf{x}_i \theta)] \frac{\textbf{x}_i}{\gamma(\phi)} = 0_k \] On peut constater que ce système n’est linéaire que si \(b'(a)=a\), c’est-à-dire si on est dans le cas du modèle linéaire. Pour tous les autres modèles linéaires généralisés, (9.3) est un système non linéaire en \(\theta\) et il n’existe pas de formule analytique pour cet estimateur. Il est cependant possible de montrer que le problème associé à la détermination de \(\hat\theta_{\scriptsize MV}\) est un problème d’optimisation convexe qui peut donc être traité par un algorithme de type Newton-Raphson, adapté à un cadre statistique, cf l’Annexe des rappels A.3 pour les détails de cet algorithme.

9.3.2 Algorithmes de Newton-Raphson et Fisher-scoring

L’algorithme de Newton-Raphson est un algorithme itératif basé sur le développement de Taylor à l’ordre 1 du score. Il fait donc intervenir la matrice Hessienne de la log-vraisemblance \[\mathcal{J}_{j\ell} = \frac{\partial^2 l(\underline{y};\theta)}{\partial\theta_j \partial\theta_\ell}.\] Il faut que \(\mathcal{J}\) soit inversible et comme elle dépend de \(\theta\), il convient de mettre à jour cette matrice à chaque étape de cet algorithme itératif. Cet algorithme est implémenté dans la plupart des logiciels statistiques.

Algorithme de Newton-Raphson

• Initialisation: \(u^{(0)}\).
• Pour tout entier \(h\) \[\begin{equation} \tag{9.4} u^{(h)} = u^{(h-1)} - [\mathcal{J}^{(h-1)}]^{-1} S(\underline{Y};u^{(h-1)}). \end{equation}\]
• Arrêt quand \[| u^{(h)} - u^{(h-1)}| \leq \Delta.\]
• on pose \(\hat\theta_{\scriptsize MV}=u^{(h)}\).

Parfois, au lieu d’utiliser la matrice hessienne, on utilise la matrice d’information de Fisher \[ \mathcal{I}_n(\theta)_{j,\ell} = -\mathbb{E}\left[ \frac{\partial^2}{\partial\theta_j \partial\theta_\ell} l(\underline{Y};\theta) \right]. \] C’est l’algorithme de Fisher-scoring. Ici aussi, on a besoin que \(\mathcal{I}_n(\theta)\) soit inversible, quitte à imposer des contraintes sur \(\theta\). Cette solution peut permettre d’éviter des problèmes de non inversibilité de la hessienne.

9.3.3 Equations de vraisemblance

Les algorithmes de type Newton-Raphson précédents nécessitent d’évaluer le score et la matrice d’information de Fisher.

Proposition 9.2 Soit le score \(S(\underline{Y};\theta) = \left(S_1,\ldots,S_k\right)'\) avec \(S_j= \frac{\partial}{\partial \theta_j} l(\underline{Y};\theta)\). Alors pour \(j\in\{1,\ldots,k\}\), \[\begin{equation} S_j = \sum_{i=1}^n \frac{(Y_i-\mu_i)x_{i}^{(j)}}{\text{Var}(Y_i)}\ \frac{\partial\mu_i}{\partial\eta_i} \tag{9.5} \end{equation}\] et \(\mathbb{E}[S_j]=0\).

La preuve est donnée en annexe B.6.

Proposition 9.3 La matrice d’information de Fisher s’écrit \[ \mathcal{I}_n(\theta)=\mathbf{X'WX} \] où \(\mathbf{W}\) est la matrice diagonale de “pondération” : \[ [\mathbf{W}]_{ii}=\frac{1}{\text{Var}(Y_i)}\left(\frac{\partial\mu_i}{\partial\eta_i}\right)^2. \]

Exercise 9.2 On rappelle que \(\mathcal{I}_n(\theta)\) est la matrice de variance-covariance de \(S(\underline{Y};\theta)\) donc \(\left(\mathcal{I}_n(\theta)\right)_{j\ell}=\mathbb{E}[S_j S_\ell]\). En utilisant (9.5), démontrez la Proposition 9.3.

Corollary 9.1 Dans le cas particulier où la fonction lien est le lien canonique associé à la structure exponentielle alors \(\eta_i = \omega_i=\mathbf{x}_i\theta\). On obtient donc les simplifications suivantes : \[ \frac{\partial\mu_i}{\partial\eta_i} = \frac{\partial\mu_i}{\partial\omega_i}=b''(\omega_i) = \frac{Var(Y_i)}{\gamma(\phi)}. \] Ainsi, \[ S_j =\sum_{i=1}^n \frac{(Y_i-\mu_i)}{\gamma(\phi)}x_{i}^{(j)} \textrm{ et } W_{ii}=\frac{Var(Y_i)}{\gamma(\phi)^2}. \] En particulier, comme \(\mathcal{I}_n(\theta)\) ne dépend plus de \(Y_i\), la hessienne est égale à la matrice d’information de Fisher et donc les méthodes de résolution du score de Fisher et de Newton-Raphson coïncident.

Si de plus \(\gamma(\phi)\) est une constante pour les observations, \[ S_j = \frac{1}{\gamma(\phi)} \underset{i=1}{\stackrel{n}{\sum}} (Y_i - \mu_i) x_i^{(j)} = 0\ \forall j \iff X' Y = X' \mu. \] Dans le cas gaussien, comme \(\mu=X\theta\) avec la fonction de lien canonique identité, on retrouve la solution \((X'X)^{-1} X'Y = \theta\) qui coincide avec celle obtenue par minimisation des moindres carrés.

9.4 Loi asymptotique de l’EMV et inférence

De part la complexité du modèle linéaire généralisé, l’obtention d’un intervalle de confiance va nécessiter un peu plus de travail que dans un cadre de statistique paramétrique usuel.

Le théorème suivant donne des propriétés sur l’estimateur du maximum de vraisemblance \(\hat \theta_{\scriptsize MV}\).

Theorem 9.1 Sous certaines conditions de régularité de la densité de probabilité, l’EMV vérifie les propriétés suivantes :

• \(\hat \theta_{\scriptsize MV}\) converge en probabilité vers \(\theta\in\mathbb{R}^k\)
• \(\hat \theta_{\scriptsize MV}\) converge en loi vers une loi gaussienne : \[\mathcal{I}_n(\theta)^{1/2} (\hat \theta_{\scriptsize MV} - \theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal{L}}{\longrightarrow}} \mathcal{N}(0_k,I_k)\]
• La statistique de Wald \(\mathcal{W}\) vérifie \[\mathcal{W}:=(\hat\theta_{\scriptsize MV} - \theta)' \mathcal{I}_n(\theta) (\hat\theta_{\scriptsize MV} - \theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal{L}}{\longrightarrow}} \chi^2(k).\]

Dans le cas particulier où la distribution des \(Y_i\) est gaussienne et la fonction de lien est canonique, il est possible de montrer que l’estimateur du maximum de vraisemblance est lui aussi gaussien et ce sans avoir recours à l’approximation \(\hat \theta_{\scriptsize MV} - \theta \stackrel{\mathcal{L}}{\simeq} \mathcal{N}(0_k,\mathcal{I}_n(\theta)^{-1})\) quand \(n\rightarrow +\infty\). Si maintenant les erreurs ne sont pas gaussiennes, le résultat précédent propose une alternative intéressante aux tests de Fisher. Ce théorème permet déjà de répondre à des problèmes intéressants comme la construction d’intervalles de confiance pour les \(\theta_j\), tests sur des valeurs de \(\theta\),…. D’autres approches complémentaires sont disponibles pour ce type de modèle, la plus connue étant basée sur le test du rapport de vraisemblance.

A noter qu’un tel résultat n’est pas utilisable tel quel puisque la matrice \(\mathcal{I}_n(\theta)\) est inconnue. Mais en remplaçant \(\mathcal{I}_n(\theta)\) par \(\mathcal{I}_n(\hat\theta_{\scriptsize MV})\) avec \(\hat \theta_{\scriptsize MV}\) converge en probabilité vers \(\theta\), on obtient que

\[ \mathcal{I}_n(\hat \theta_{\scriptsize MV})^{1/2} (\hat \theta_{\scriptsize MV} - \theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal{L}}{\longrightarrow}} \mathcal{N}(0_k,I_k) \] et \[ (\hat\theta_{\scriptsize MV} - \theta)' \mathcal{I}_n(\hat \theta_{\scriptsize MV}) (\hat\theta_{\scriptsize MV} - \theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal{L}}{\longrightarrow}} \chi^2(k). \]

9.5 Tests d’hypothèses

Contrairement au cas du modèle linéaire, la loi de l’estimateur du maximum de vraisemblance dans le cadre du modèle linéaire généralisé n’est connue qu’asymptotiquement. Aussi les procédures de test vont être menées dans un cadre asymptotique. Nous allons dans la suite considérer plusieurs problèmes de test qui permettent d’examiner la qualités du modèle, de déterminer si les différentes variables explicatives du modèles sont pertinentes ou pas, ….

9.5.1 Test de modèles emboîtés

Le test de comparaison des modèles emboîtés permet de déterminer si un sous-ensemble de variables explicatives est suffisant pour expliquer la réponse \(Y\) comme dans le cas du modèle linéaire.

On considère deux modèles emboîtés \(M_1\) et \(M_0\), définis par \(g(\mu)=X_1\theta_1\) et \(g(\mu)=X_0\theta_0\) respectivement, avec \(M_0\) sous-modèle de \(M_1\).

9.5.1.1 Test du rapport de vraisemblance

Pour traiter ce problème, on peut considérer le test du rapport de vraisemblance.

Proposition 9.4 La statistique de test du test du rapport de vraisemblance est définie par \[ T=-2 \ln\left[\frac{L(\underline{Y};\hat \theta_0)}{L(\underline{Y};\hat \theta_1)}\right] = -2 \left[l(\underline{Y};\hat \theta_0) - l(\underline{Y};\hat \theta_1)\right] \] où \(\hat \theta_0\) et \(\hat \theta_1\) sont les EMV de \(\theta\) dans le modèle \(M_0\) et \(M_1\) respectivement.

Sous certaines conditions, on peut montrer que \[ T\underset{n\rightarrow +\infty}{\stackrel{\mathcal{L}}{\rightarrow}} \chi^2(k_1-k_0) \] où \(k_0\) et \(k_1\) sont les dimensions des sous-espaces engendrés par les colonnes de \(X_0\) et \(X_1\) respectivement.

La zone de rejet est alors définie par \[ \mathcal{R}_\alpha = \{T> v_{1-\alpha,k_1-k_0}\} \] où \(v_{1-\alpha,k_1-k_0}\) est le \((1-\alpha)\)- quantile de la loi du \(\chi^2\) à \(k_1-k_0\) degrés de liberté.

Ce test est parfois présenté de façon un peu différente en faisant intervenir la déviance.

Definition 9.2 La déviance d’un modèle d’intérêt \(M\) est l’écart entre la log-vraisemblance du modèle \(M\) et celle du modèle le plus complet possible \(M_{sat}\), appelé modèle saturé. Le modèle saturé est le modèle comportant \(n\) paramètres, c’est à dire autant que d’observations. La déviance de \(M\) est définie par : \[ \mathcal{D}(M)= -2\left[l(\underline{Y}; \hat \theta) - l(\underline{Y}; \hat \theta_{sat})\right]. \]

Ainsi la statistique de test \(T\) peut se réécrire avec la déviance sous la forme \[ T = \mathcal D(M_0) - \mathcal D(M_1). \]

9.5.1.2 Test de Wald

Comme dans le modèle linéaire, on peut reformuler les hypothèses et vouloir tester

\[ \mathcal H_0: C \theta = 0_q \textrm{ contre } \mathcal H_1: C \theta \neq 0_q \] où \(C\in \mathcal M_{qk}(\mathbb{R})\) (définie l’ensemble \(\mathcal{H}_0\) des hypothèses à tester sur les paramètres correspondant à \(q\) contraintes).

Proposition 9.5 Connaissant la loi asymptotique de \(\hat \theta_{\scriptsize MV}\), on obtient que \[ \left[C \mathcal{I}_n(\hat\theta_{\scriptsize MV})^{-1} C' \right]^{-1/2} (C\hat \theta_{\scriptsize MV} - C\theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal L}{\longrightarrow}} \mathcal N(0_q,I_q) \] et \[ (C\hat \theta_{\scriptsize MV} - C\theta)' \left[C \mathcal{I}_n(\hat\theta_{\scriptsize MV})^{-1} C'\right]^{-1} (C\hat \theta_{\scriptsize MV} - C\theta) \underset{n\rightarrow +\infty}{\stackrel{\mathcal L}{\longrightarrow}} \mathcal \chi^2(q). \] On considère donc la zone de rejet \[\mathcal R_\alpha = \{ (C\hat \theta_{\scriptsize MV} )' \left[C \mathcal{I}_n(\hat\theta_{\scriptsize MV})^{-1} C'\right]^{-1} (C\hat \theta_{\scriptsize MV}) > v_{1-\alpha,q} \}\] où \(v_{1-\alpha,q}\) est le \((1-\alpha)\) quantile d’un \(\chi^2(q)\).

Ce test est appelé test de Wald.

Le test de Wald est basé sur la forme quadratique faisant intervenir la matrice de covariance des paramètres, l’inverse de la matrice d’information observée \((X'WX)^{-1}\). Cette matrice généralise la matrice \((X'X)^{-1}\) utilisée dans le cas du modèle linéaire gaussien en faisant intervenir une matrice \(W\) de pondération. Ainsi, les test de Wald et test de Fisher sont équivalents dans le cas particulier du modèle gaussien. Attention, le test de Wald peut ne pas être précis si le nombre d’observations est faible.

9.5.2 Test d’un paramètre \(\theta_j\)

On s’intéresse ici à tester quelles sont les variables qui ont une influence. On revient au problème général de vouloir tester \(\mathcal H_0: \theta_j = a\) contre \(\mathcal H_0: \theta_j \neq a\), où \(a\) est une valeur définie a priori (souvent \(a=0\)).

Proposition 9.6 D’après le théorème 9.1, on peut faire l’approximation de loi suivante sous \(\mathcal{H}_0\) : \[ (\hat \theta_{\scriptsize MV})_j - a \underset{\mathcal{H}_0}{\stackrel{\mathcal L}{\simeq}} \mathcal{N}\left(0,[\mathcal{I}_{n}(\hat \theta_{\scriptsize MV})^{-1}]_{jj}\right). \] On va donc rejeter \(\mathcal{H}_0\) si \[ T_j := \left| (\hat \theta_{\scriptsize MV})_j - a \right| / \sqrt{[\mathcal{I}_{n}(\hat \theta_{\scriptsize MV})^{-1}]_{jj}} > z_{1-\alpha/2} \] où \(z_{1-\alpha/2}\) est le \(1-\alpha/2\) quantile de la loi \(\mathcal N(0,1)\).

Ce test est appelé le Z-test.

Remark. Ce test est équivalent au test de Wald : on rejette \(\mathcal{H}_0\) si \[ \left[ (\hat \theta_{\scriptsize MV})_j - a \right]^2 / [\mathcal{I}_{n}(\hat \theta_{\scriptsize MV})^{-1}]_{jj} > v_{1-\alpha,1} \]
où \(v_{1-\alpha,1}\) est le \(1-\alpha\) quantile de la loi \(\chi^2(1)\).

9.6 Intervalle de confiance pour \(\theta_j\)

9.6.1 Par Wald

D’après le théorème 9.1, on peut faire l’approximation de loi suivante : \[ \left[ (\hat \theta_{\scriptsize MV})_j - \theta_j \right] / \sqrt{[\mathcal{I}_{n}(\hat\theta_{\scriptsize MV})^{-1}]_{jj}} \underset{n\rightarrow +\infty}{\stackrel{\mathcal L}{\longrightarrow}} \mathcal{N}\left(0, 1 \right). \] On peut donc construire l’intervalle de confiance asymptotique pour \(\theta_j\) au niveau de confiance \(1-\alpha\) suivant : \[ IC_{1-\alpha}(\theta_j) = \left [ (\hat \theta_{\scriptsize MV})_j \pm z_{1-\alpha/2} \sqrt{[\mathcal{I}_{n}(\hat\theta_{\scriptsize MV})^{-1}]_{jj}} \right] \] où \(z_{1-\alpha/2}\) est le \(1-\alpha/2\) quantile de la loi \(\mathcal N(0,1)\).

9.6.2 Fondé sur le rapport de vraisemblances

La fonction de vraisemblance profil de \(\theta_j\) est définie par \[ l^\star(\underline{Y}; \theta_j) = \underset{\tilde\theta}{\max}\ l(\underline{Y}; \tilde\theta) \] où \(\tilde\theta\) est le vecteur \(\theta\) avec le \(j\)ème élément fixé à \(\theta_j\). Si \(\theta_j\) est la vraie valeur du paramètre alors \[ 2 \left[ l(\underline{Y}; \hat\theta_{\scriptsize MV}) - l^\star(\underline{Y}; \theta_j) \right] \underset{n\rightarrow +\infty}{\stackrel{\mathcal L}{\longrightarrow}} \chi^2(1). \] Ainsi, si on considère l’ensemble \[ \mathcal G=\left\{u; 2 \left[ l(\underline{Y}; \hat\theta_{\scriptsize MV}) - l^\star(\underline{Y}; u) \right] \leq v_{1-\alpha,1} \right\}, \] on obtient que \(\mathbb{P}(\theta_j\in\mathcal G) \underset{n\rightarrow +\infty}{\longrightarrow} 1-\alpha\). Ainsi \(\mathcal G\) est un intervalle de confiance asymptotique pour \(\theta_j\) au niveau de confiance \(1-\alpha\).

9.7 Qualité d’ajustement

9.7.1 Le pseudo \(R^2\)

Definition 9.3 Le pseudo-\(R^2\) d’un modèle d’intérêt \(M\) est défini par \[ pseudoR^2 = \frac{\mathcal D(M_0)-\mathcal D(M)}{\mathcal D(M_0)}. \] où \(M_0\) est le modèle nul (juste un intercept).

Cette définition est obtenue par analogie avec le \(R^2=1-\frac{SSR}{SST}\) utilisé dans le cadre du modèle linéaire. En effet, on rappelle que \(SST\) est la somme des carrés des résidus pour le modèle nul \(M_0\). Ce pseudo-\(R^2\) varie entre \(0\) et \(1\). Plus il est proche de \(1\), meilleur est l’ajustement du modèle.

9.7.2 Le \(\chi^2\) de Pearson généralisé

Le \(\chi^2\) de Pearson généralisé est la statistique définie par \[ Z^2=\sum_{i=1}^{n}\frac{(Y_i-\hat \mu_i)^2}{\mbox{Var}_{\widehat\mu_i}(Y_i)} \] où \(\hat \mu_i= g^{-1}(\textbf{x}_i\hat \theta_{\scriptsize MV})\) et \(\mbox{Var}_{\widehat\mu_i}(Y_i)= \mbox{Var}_{\mu}(Y_i)|_{\mu=\widehat\mu_i}\) ( la variance théorique de \(Y_i\) évaluée en \(\hat \mu_i\)).

Sous l’hypothèse que le modèle étudié est le bon modèle et si l’approximation asymptotique est valable, alors la loi de \(Z^2\) est approchée par \(\chi^2(n-k)\). On rejette donc le modèle étudié au niveau \(\alpha\) si la valeur observée de \(Z^2\) est supérieure au \((1-\alpha)\) quantile de la loi \(\chi^2(n-k)\).

9.8 Diagnostic, résidus

Dans le modèle linéaire généralisé, la définition la plus naturelle pour le résidu consiste à quantifier l’écart entre \(Y_i\) et sa prédiction par le modèle \(\hat \mu_i\). On définit ainsi les résidus bruts \(\varepsilon_i = Y_i - \hat \mu_i\). Mais ces résidus n’ayant pas toujours la même variance, il est difficile de les comparer à un comportement type attendu. Par exemple dans le cas d’un modèle de Poisson, l’écart-type d’un effectif est \(\sqrt{\hat \mu_i}\), de grosses différences tendent à apparaitre quand \(\mu_i\) prend des valeurs élevées. En normalisant les résidus bruts par une variance estimée, on obtient les résidus “standardisés” de Pearson : \[ r_{Pi} = \frac{Y_i - \hat \mu_i}{\sqrt{Var_{\hat\mu_i}(Y_i)}}. \] On remarque que la somme des carrés des \(r_{Pi}\) correspond au \(\chi^2\) de Pearson généralisé.

On peut également étudier les résidus déviance définis par : \[ r_{Di}=\sqrt{d_i}\ sgn(Y_i - \hat \mu_i) \] où \(d_i\) représente la contribution de l’observation \(i\) à la déviance \(\mathcal D\).

Du fait que les résidus sont calculés sur les données de l’échantillon qui ont permis de construire le modèle, on risque de sous-estimer les résidus. En notant \(h_i\) le levier associé à l’observation \(i\), \(i\)ème terme diagonal de la matrice \(H=\mathbf{W}^{1/2}\mathbf{X(X'WX)}^{-1}\mathbf{X'}\mathbf{W}^{1/2}\), on définit alors :

• le résidu de Pearson normalisé : \[r_{Pi}^\star = \frac{Y_i - \hat \mu_i}{\sqrt{Var_{\hat\mu_i}(Y_i)(1-h_i)}}\]
• le résidu déviance normalisé : \[r_{Di}^\star = \frac{\sqrt{d_i}\ sgn(Y_i - \hat \mu_i)}{\phi(1-h_i)}\]
• le résidu vraisemblance normalisé : \[r_{Gi}=sgn(Y_i-\hat\mu_i) \sqrt{(1-h_i) r_{Di}^{\star\ 2} + h_i r_{Pi}^{\star\ 2}}\]

9.9 En résumé

• Savoir modéliser un MLG en précisant bien les 3 parties (compo. aléatoire, compo. linéaire, fonction de lien)
• Savoir montrer qu’une loi fait partie de la famille exponentielle (la définition n’est pas à connaitre, elle sera rappelée si besoin)
• Connaitre la fonction de lien canonique pour les lois gaussienne, Bernoulli et Poisson
• Comprendre l’esprit général pour déterminer un estimateur du vecteur des paramètres en MLG
• Connaitre le théorème sur la loi de l’estimateur \(\hat\theta_{{\scriptsize MV}}\) en MLG
• Savoir construire un test de modèles emboités, un test de Wald et un \(Z\)-test
• Construire un IC pour \(\theta_j\) par Wald
• Connaitre la définition du pseudo-\(R^2\)

References

Agresti, Alan. 2003. Categorical Data Analysis. Vol. 482. John Wiley & Sons.

Antoniadis, Anestis, Jacques Berruyer, and René Carmona. 1992. Régression Non Linéaire et Applications. Economica.

McCullagh, Peter. 2018. Generalized Linear Models. Routledge.