Chapitre 1 Introduction
Documents associés à ce chapitre :
- Les slides associés à ce chapitre sont disponibles ici: SlidesIntro.pdf
- Le jeu de données utilisé est
ronfletabac.csv
Dans ce chapitre nous allons introduire à travers plusieurs exemples les différents types de modèles linéaires (général et généralisé) que nous allons aborder dans ce cours.
1.1 Modélisation d’une réponse quantitative
1.1.1 Jeu de données illustratif
On considère le jeu de données ronfletabac.csv.
Pour 100 individus, on dispose de leur taille, leur poids, leur âge et leur sexe (75 hommes et 25 femmes). On sait également si ce sont des fumeurs ou non; s’ils ronflent la nuit ou non. On appelle don le jeu de données chargé sous R.
Un extrait des données est présenté ci-dessous :
On obtient le résumé suivant des données :
age weight height sex snore tobacco
Min. :23.00 Min. : 42.00 Min. :158.0 F:25 N:65 N:36
1st Qu.:43.00 1st Qu.: 75.50 1st Qu.:166.0 H:75 O:35 O:64
Median :52.00 Median : 92.00 Median :186.0
Mean :52.27 Mean : 88.83 Mean :181.1
3rd Qu.:62.25 3rd Qu.:104.25 3rd Qu.:194.0
Max. :74.00 Max. :120.00 Max. :208.0 Ce jeu de données est donc composé de 3 variables quantitatives et 3 variables qualitatives. Pour les variables quantitatives age, weights et height, leur distribution est résumée en Figure 1.1.
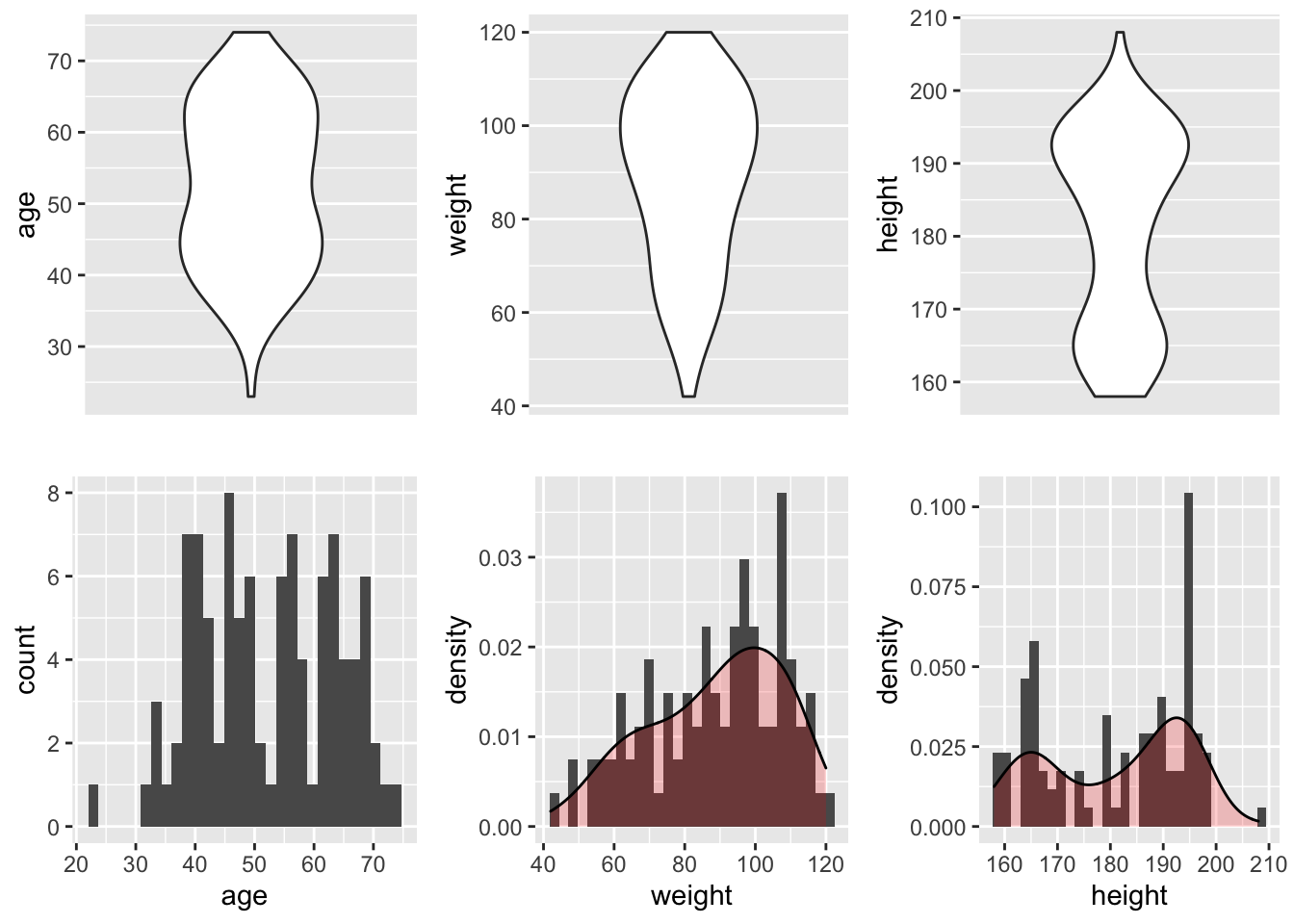
Figure 1.1: Représentations graphiques de la distribution des variables quantitatives : l’âge, le poids et la taille.
Pour les variables qualitatives sex, tobacco et snore, on résume les données sous forme de tableau de fréquences (Table 1.1) et on les présente graphiquement par des diagrammes en bâtons (Figure 1.2).
| Variable | Modalités | Fréquence en % |
|---|---|---|
| Sex | Féminin | 25 |
| Masculin | 75 | |
| Tobacco | Oui | 64 |
| Non | 36 | |
| Snore | Oui | 35 |
| Non | 65 |
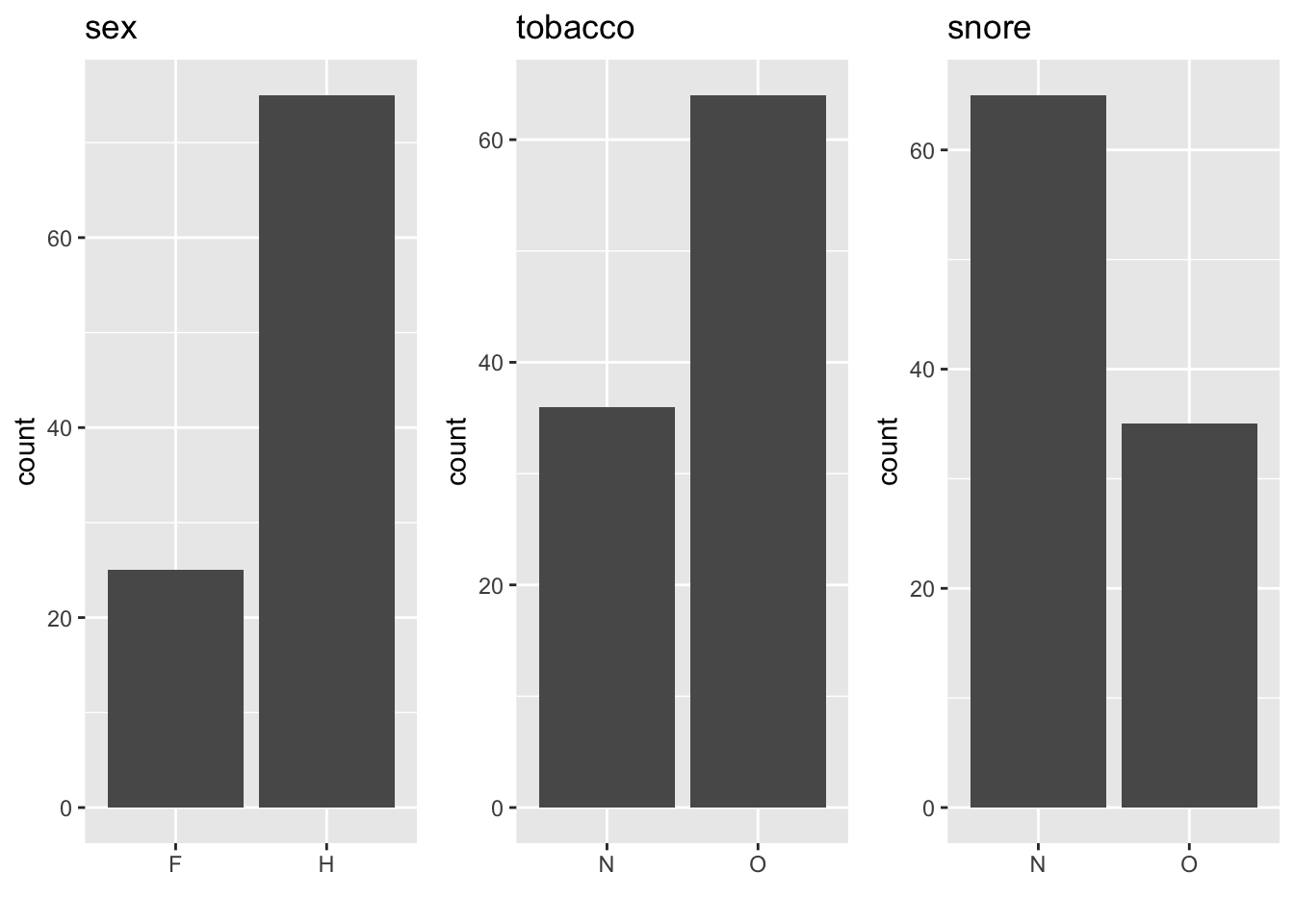
Figure 1.2: Diagrammes en bâtons représentant la distribution des variables qualitatives : sexe, tabac et ronfle.
1.1.2 Régression linéaire
Pour étudier la relation entre deux variables quantitatives (par exemple, entre le poids et la taille, ou entre le poids et l’âge), on peut tracer un nuage de points (Figure 1.3) et calculer le coefficient de corrélation linéaire entre ces deux variables (Table 1.2).
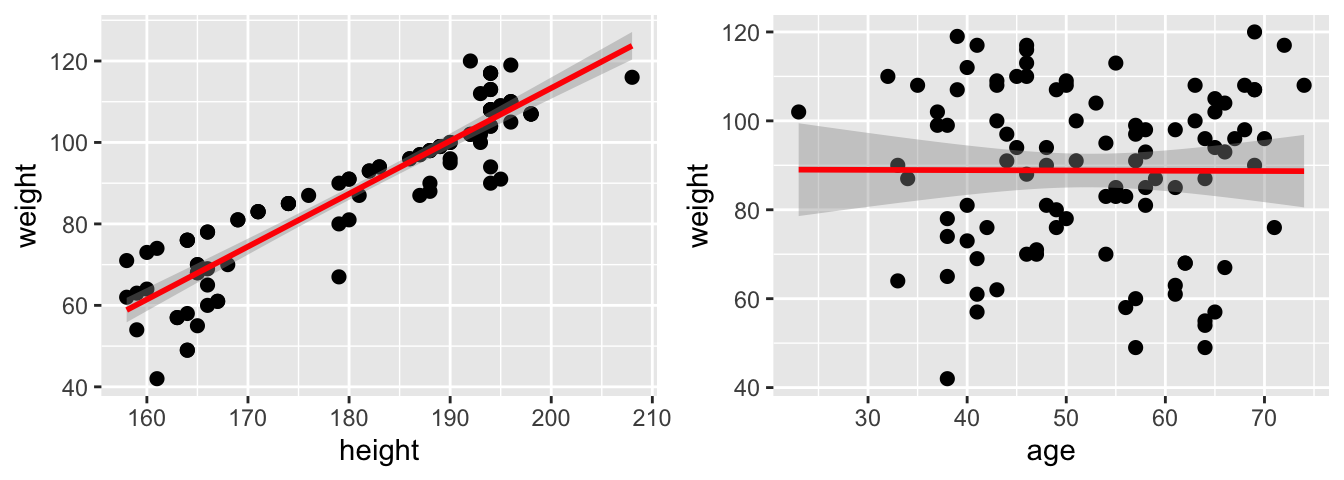
Figure 1.3: Nuage de points représentant la relation entre le poids et la taille (à gauche), entre le poids et l’âge (à droite).
Nous remarquons que le coefficient de corrélation linéaire est significativement différent de 0 entre le poids et la taille. Ce n’est pas le cas entre le poids et l’âge.
| height | age | |
|---|---|---|
| weight | 0.92 | -0.004 |
| pvaleur | <2.2e-16 | 0.9687 |
1.1.2.1 Régression linéaire simple
Le nuage de points peut être résumé par une droite que l’on appellera la droite de régression linéaire simple. C’est le cas le plus simple de modèle linéaire, qui permet d’expliquer une variable quantitative en fonction d’une autre variable quantitative. Par exemple, la droite de régression linéaire résumant la relation entre le poids et la taille a pour équation : \[\begin{equation} weight_i= a + b \times height_i + \varepsilon_i, \, i=1,\cdots, 100 \label{eq:eqreglin} \end{equation}\] où \(\varepsilon_i\) désigne l’erreur associée à chaque observation. Généralement, ces erreurs sont supposées être des variables indépendantes gaussiennes centrées de variance constante \(\sigma^2\) à estimer.
Le modèle statistique sous-jacent à l’équation peut aussi être présenté sous une forme matricielle :
\[\begin{equation} \underbrace{\left(\begin{array}{c}weight_1 \\ \vdots \\ weight_{100}\end{array} \right)}_{weight} = \underbrace{\left( \begin{array}{cc} 1 & height_1 \\ \vdots & \vdots\\ 1 & height_{100} \end{array} \right)}_{X} \underbrace{\left( \begin{array}{c} a \\ b \end{array} \right)}_{\theta} + \underbrace{\left( \begin{array}{c} \varepsilon_1 \\ \vdots \\ \varepsilon_{100} \end{array} \right)}_{\varepsilon} \tag{1.1} \end{equation}\]
Dans le modèle (1.1), \(\theta=(a,b)'\) et \(\sigma^2\) sont inconnus. Afin d’estimer les paramètres \(a\) et \(b\), nous utilisons la méthode des moindres carrés. Nous choisissons ainsi le couple \((\hat a, \hat b)\) vérifiant : \[(\hat a, \hat b)= \mathrm{arg} \underset{(\alpha,\beta)}{\mathrm{min} } \sum_{i=1}^{100} \left( weight_i - \alpha\ - \beta\ height_i \right)^2=\mathrm{arg} \underset{(\alpha,\beta)}{\mathrm{min} }\ || weight -\alpha \mathbb{1}_{100} - \beta\ height ||^2.\]
Dans le chapitre dédié à la régression linéaire, nous déterminerons l’expression explicite de ces estimateurs et étudierons leurs propriétés. A l’aide de la fonction lm() sous R, on peut facilement ajuster ce modèle de régression linéaire sur les données :
Call:
lm(formula = weight ~ height, data = don)
Residuals:
Min 1Q Median 3Q Max
-20.7482 -3.8787 0.6629 4.1182 17.0261
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -146.16586 10.35384 -14.12 <2e-16 ***
height 1.29760 0.05702 22.76 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.583 on 98 degrees of freedom
Multiple R-squared: 0.8409, Adjusted R-squared: 0.8393
F-statistic: 517.9 on 1 and 98 DF, p-value: < 2.2e-16En pratique nous obtenons les estimations suivantes :
- \(\left(\widehat{b}\right)^{obs} =\) 1.298 : estimation de la pente de la droite de régression = estimation de la variation moyenne du poids par rapport à la taille
- \(\left(\widehat{a}\right)^{obs} =\) -146.166 : estimation de l’ordonnée à l’origine de la droite de régression
- \(\left(\widehat{\sigma^2}\right)^{obs}=\) (7.583)\(^2\)
L’estimation de la pente égale à 1.298 est significativement différente de 0, montrant que le poids et la taille sont liés de façon significative.
Ces résultats préliminaires ne donnent qu’une approximation du modèle linéaire sous-jacent. Dans bien des situations, il reste à mener une étude approfondie permettant de “valider” le modèle et de l’exploiter (construction de tests, d’intervalles de confiance, …) Nous reviendrons plus en détails sur ces notions dans les chapitres suivants.
1.1.2.2 Régression linéaire multiple
Il peut être également intéressant de modéliser une variable en fonction de plusieurs autres variables quantitatives, par un modèle de régression linéaire multiple. Par exemple, on peut modéliser le poids en fonction de la taille et de l’âge, ce qui donne l’équation suivante : \[weight_i = a_0 + a_1 \times height_i + a_2 \times age_i + \varepsilon_i,\] où les \(\varepsilon_i\), \(i=1,\ldots,100\) désignent des variables indépendantes gaussiennes centrées de variance constante \(\sigma^2\).
Dans ce cas, le modèle statistique peut s’écrire de la façon suivante :
\[\begin{equation} \underbrace{\left( \begin{array}{c} weight_1 \\ \vdots \\ weight_{100} \end{array} \right)}_{weight} =\underbrace{\left( \begin{array}{ccc} 1 & height_1 & age_1\\ \vdots & \vdots & \vdots \\ 1 & height_{100} & age_{100} \end{array} \right)}_{X} \underbrace{\left( \begin{array}{c} \theta_0 \\ \theta_1 \\\theta_2 \end{array} \right)}_{\theta} +\underbrace{\left( \begin{array}{c} \varepsilon_1 \\ \vdots \\ \varepsilon_{100} \end{array} \right)}_{\varepsilon} \tag{1.2} \end{equation}\]
cette formule pouvant à nouveau être écrite de la façon suivante : \(weight=X\theta + \varepsilon\).
On peut remarquer en regardant les équations (1.1) et (1.2) que les deux modèles de régression linéaire considérés précédemment s’écrivent sous une “même forme” matricielle.
1.1.3 Analyse de la variance (ANOVA)
Il est possible d’étudier la relation entre une variable quantitative et une variable qualitative, par exemple entre le poids et le sexe, ou entre le poids et le tabac. Cette relation est représentée graphiquement par des violin plots (ou boxplots) parallèles (Figure 1.4).
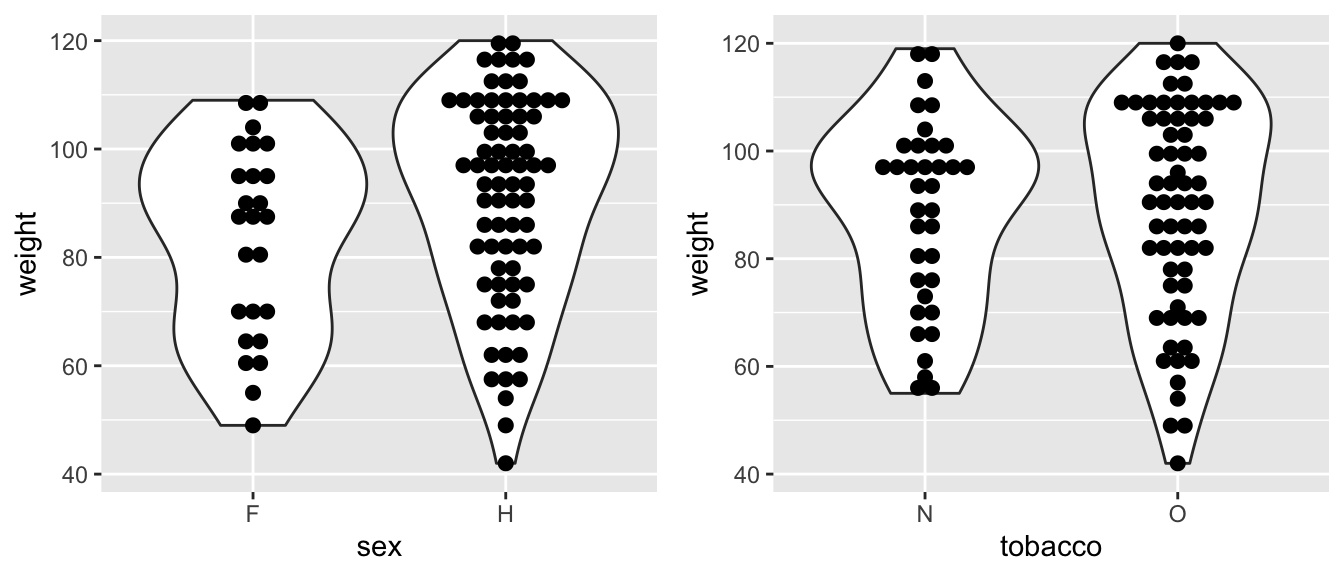
Figure 1.4: Boxplots parallèles représentant la relation entre le poids et le sexe (à gauche); entre le poids et le tabac (à droite).
1.1.3.1 ANOVA à un facteur
Intuitivement, pour comparer le poids des hommes et celui des femmes, nous allons calculer le poids moyen pour chaque groupe. Statistiquement, nous modélisons le poids en fonction du sexe en mettant en oeuvre un modèle d’analyse de variance à un facteur qui s’écrit sous la forme : \[weight_i = \mu_1 \mathbb{1}_{sex_i=F} + \mu_2\mathbb{1}_{sex_i=H} +\varepsilon_i,\] où les \(\varepsilon_i, \, i=1,\ldots,100\) désignent des variables indépendantes gaussiennes centrées de variance constante \(\sigma^2\). Dans ce cas, en réordonnant les observations selon le facteur sexe, le modèle peut être écrit sous la forme matricielle suivante : \[\underbrace{\left( \begin{array}{c} weight_{11} \\ \vdots \\ weight_{1n_1} \\ weight_{21} \\ \vdots \\ weight_{2n_2} \end{array} \right)}_{weight} = \underbrace{\left( \begin{array}{cc} 1 & 0 \\ \vdots & \vdots \\ 1 & 0 \\ 0 & 1 \\ \vdots & \vdots \\ 0 & 1 \end{array} \right)}_{X} \underbrace{\left( \begin{array}{c} \mu_1 \\ \mu_2 \end{array} \right) }_{\theta} +\underbrace{ \left( \begin{array}{c} \varepsilon_{11} \\ \vdots \\ \varepsilon_{1n_1} \\ \varepsilon_{21} \\ \vdots \\ \varepsilon_{2n_2} \end{array} \right)}_{\varepsilon},\] où \(weight_{ij}\) désigne le poids de l’individu \(j\) de sexe \(i=F\) ou H avec \(j\) variant de \(1\) à \(n_i\).
En pratique, on utilise la méthode des moindres carrés pour estimer les paramètres inconnus. Toujours à l’aide de la fonction lm() de R, on obtient les résultats suivants :
Call:
lm(formula = weight ~ sex - 1, data = don)
Residuals:
Min 1Q Median 3Q Max
-48.77 -13.44 4.00 16.23 29.23
Coefficients:
Estimate Std. Error t value Pr(>|t|)
sexF 83.000 3.741 22.19 <2e-16 ***
sexH 90.773 2.160 42.03 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18.7 on 98 degrees of freedom
Multiple R-squared: 0.9584, Adjusted R-squared: 0.9576
F-statistic: 1129 on 2 and 98 DF, p-value: < 2.2e-16Nous obtenons donc \(\left(\widehat{ \mu_1}\right)^{obs} =\) 83 et \(\left(\widehat{ \mu_2}\right)^{obs}=\) 90.773 qui représentent le poids moyen des femmes et celui des hommes respectivement.
1.1.3.2 ANOVA à deux facteurs
Il est également possible d’étudier l’effet conjoint du sexe et du tabac sur le poids. Intuitivement, on peut étudier les moyennes par classe, en croisant les deux variables qualitatives. Pour étudier l’effet combiné du sexe et du tabac sur le poids, nous mettons en oeuvre un modèle d’analyse de variance à deux facteurs croisés. Ce modèle s’écrit de la façon suivante :
\[weight_{ijk} = \mu + \alpha_i + \beta_j + \gamma_{ij} + \varepsilon_{ijk},\ \varepsilon_{ijk}\underset{i.i.d}{\sim}\mathcal N (0,\sigma^2)\] où \(weight_{ijk}\) désigne le poids de l’individu \(k\) tel que \(sexe = i\in\{H,F\}\) et \(tabac=j\in\{0,N\}\). Les variables \(\varepsilon_{ijk}\) sont supposées être des variables indépendantes gaussiennes centrées et de variance constante \(\sigma^2\). Nous pouvons également écrire ce modèle sous forme matricielle de la forme \[weight=X\theta +\varepsilon.\] Ce modèle nous permettra d’étudier l’effet de chaque facteur (sexe et tabac) sur le poids, mais aussi de détecter des combinaisons (interactions) entre le sexe et le tabac qui donneraient un poids particulièrement différent des autres classes.
1.1.4 Analyse de covariance (ANCOVA)
Sur notre exemple, nous pouvons tenter d’expliquer le poids selon la taille (variable quantitative) et le sexe (variable qualitative). Dans ce cas, nous pouvons représenter deux nuages de points entre le poids et la taille, l’un pour les femmes et l’autre pour les hommes, comme le montre la Figure 1.5.
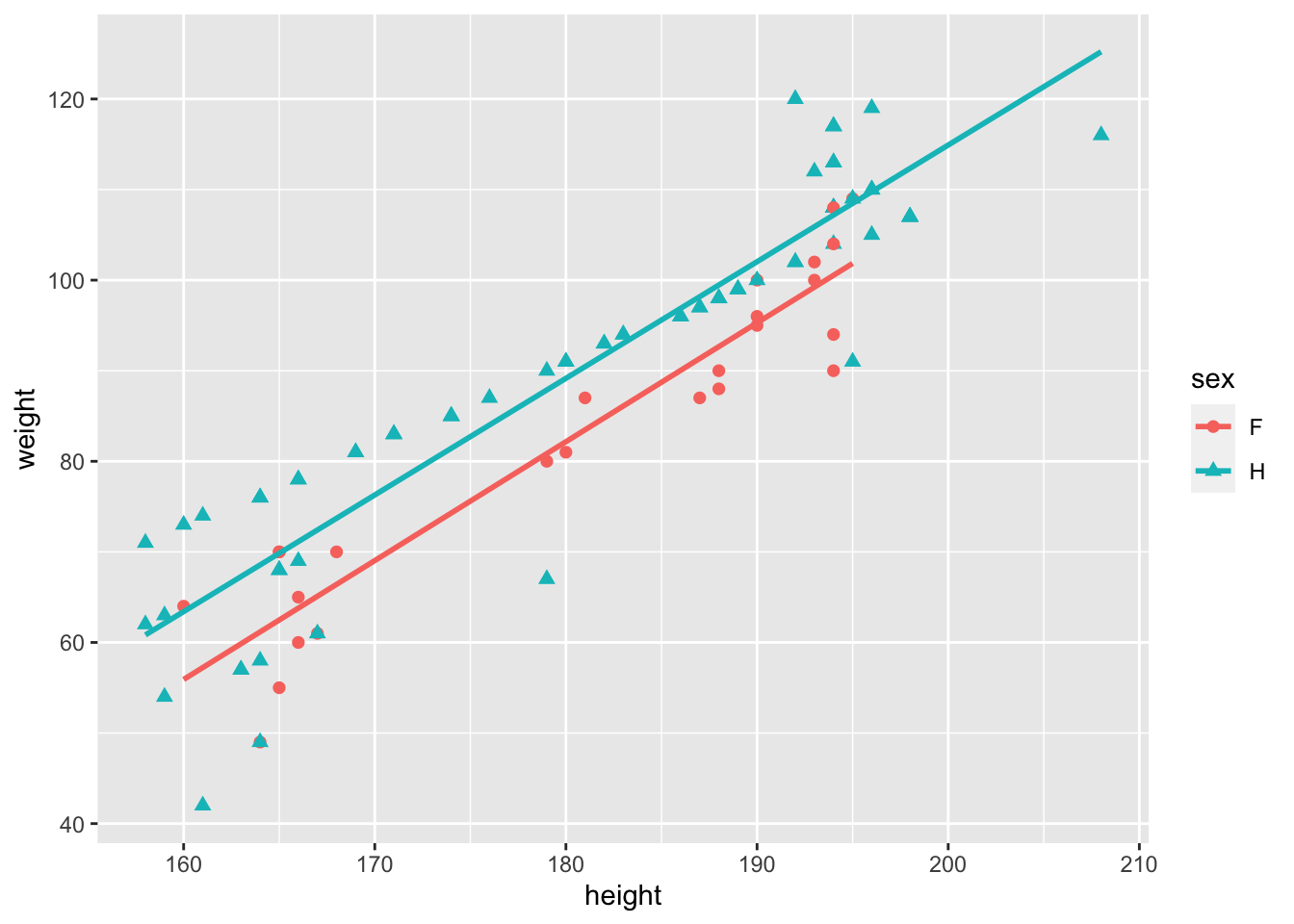
Figure 1.5: Nuages de points représentant la relation entre le poids et la taille selon le sexe.
Le modèle d’analyse de covariance s’écrit de la façon suivante : \[ weight_{ij}=a_i + b_i \ height_{ij} + \varepsilon_{ij}, i\in\{H,F\} \mbox{ et } j=1, \cdots, n_i \] où \(weight_{ij}\) désigne le poids de l’individu \(j\) de sexe \(i\) et les erreurs \(\varepsilon_{ij}\) sont supposées gaussiennes centrées indépendantes et de variance \(\sigma^2\).
Nous pouvons ainsi comparer l’effet de la taille sur le poids, selon le sexe en mettant en oeuvre un modèle d’analyse de la covariance. En pratique cela correspond à estimer, pour chaque modalité de la variable sexe, une droite de régression du poids en fonction de la taille.
En conclusion, dans les divers problèmes évoqués dans ce paragraphe, à savoir la régression linéaire, l’analyse de variance et l’analyse de covariance, nous avons utilisé :
- le même type de modélisation matricielle,
- le même type d’hypothèses sur les erreurs,
- l’estimateur des moindres carrés.
En fait, ces différents problèmes ne sont pas si éloignés qu’ils le paraissent a priori car les modèles utilisés font partie d’une même famille de modèles : le modèle linéaire général.
1.2 Modélisation d’une variable binaire, de comptage, …
On se place maintenant dans le cas où la variable réponse \(Y\) est qualitative (ou des comptages) et on souhaite expliquer cette variable \(Y\) en fonction de plusieurs régresseurs \(z^{(1)},\dots,z^{(m)}\).
Voici quelques exemples illustratifs :
Exemple 1 Une compagnie d’assurance cherche à détecter les dossiers frauduleux. Elle dispose pour cela d’un panel de \(n\) dossiers. À chacun de ces dossiers est associé la valeur \(0\) (pour dossier frauduleux) ou \(1\). Après avoir sélectionné les caractéristiques les plus intéressantes (endettement du foyer, milieu social, lieu de résidence, …), elle cherche à savoir dans quelle mesure ces dernières variables influencent la probabilité d’existence d’une fraude. Elle espère pouvoir ainsi à l’avenir détecter d’éventuels dossiers “sensibles”. On est dans le cas d’une variable réponse \(Y\) binaire.
Exemple 2 On souhaite expliquer le nombre d’espèces de plantes qui se développent dans différents lieux en fonction de la biomasse de ces différents lieux et du pH du sol. La variable réponse \(Y\) prend ici ses valeurs dans \(\mathbb{N}\).
Dans le cas d’une variable réponse binaire, on dispose d’un vecteur \(Y=(Y_1,\dots,Y_n)'\) où \(Y_i \sim \mathcal{B}(\pi_i)\) pour tout \(i\in\lbrace 1,\dots, n \rbrace\) et de \(m\) régresseurs \(z^{(1)},\dots,z^{(m)}\). Il semblerait assez naturel d’utiliser la modélisation suivante : \[\mathbb{E}[Y_i] = \pi_i = a_1 z_i^{(1)} + a_2 z_i^{(2)} + \dots + a_m z_i^{(m)}, \ i=1, \dots ,n.\] Cependant, comme on cherche à modéliser et prédire des probabilités, cette approche semble peu recommandée dans la mesure où certaines valeurs prédites pourraient ne pas appartenir à l’intervalle \([0,1]\). On va donc plutôt chercher à modéliser linéairement une fonction des \(\pi\). Par exemple dans le cadre de la régression logistique, on considère la fonction de lien \(g: ]0,1[ \rightarrow \mathbb{R}\) définie par \[ g(t) = \ln\left( \frac{t}{1-t} \right), \ \forall t\in ]0,1[\] et on modélise \[ g(\pi_i)= a_1 z_i^{(1)} + \dots + a_m z_i^{(m)}, \ \forall i \in \lbrace 1,\dots,n \rbrace.\]
De manière plus générale, il est possible d’envisager de considérer d’autres distributions pour la variable \(Y\) et d’autres fonctions de lien. À ce titre, on pourra remarquer que le modèle de régression abordé au début de ce chapitre correspond à une distribution gaussienne et à une fonction de lien canonique (identité). Nous verrons qu’il est possible d’étudier tous ces modèles à travers un même cheminement : le modèle linéaire généralisé.
1.3 Objectifs du cours
Nous verrons que les modèles de régression linéaire (simple ou multiple), d’analyse de variance et d’analyse de covariance peuvent être rassemblés sous un même formalisme : on parle alors de modèle linéaire général. Un cran au-dessus, nous pouvons encore rassembler le modèle linéaire général et par exemple la régression logistique sous une même bannière : le modèle linéaire généralisé. Les possibilités offertes par ces différentes modélisations ne s’arrêtent pas à une simple écriture commune. C’est en fait tout le traitement et l’exploitation des données qui peuvent être abordés de manière unifiée.
Les slides pour les chapitres 2, 3, 4 et 5 sont disponibles ici