Chapitre 10 Régression logistique
Les slides associés à la régression logistique sont disponibles ici (Partie I)
Le jeu de données Default utilisé pour la régression logistique est issu de la librairie
ISLR. Le jeu de données utilisé pour illustrer la régression polytomique non-ordonnée est MarqueSexe.csv Le jeu de données utilisé pour illustrer la régression polytomique ordonnée est SunRain.csvRemarque pour les étudiant-e-es de l’UF EMS : la partie sur la régression polytomique est hors programme.
10.1 Introduction
Dans ce chapitre, on s’intéresse au cas où la variable réponse \(Y\) est binaire. Nous allons illustrer les différents points abordés dans ce chapitre avec l’exemple Default issu de la librarie ISLR.
Example 10.1 Problème de défaut bancaire On s’intéresse à la variable réponse binaire default qui indique si des clients sont en défaut sur leur dette de carte de crédit (default=1 si le client fait défaut sur sa dette, 0 sinon). On considère ici un échantillon de \(n=10000\) clients et l’on souhaite expliquer la variable default à l’aide des \(3\) variables suivantes :
- student : 1 si le client est étudiant, 0 sinon
- balance : montant moyen mensuel d’utilisation de la carte de crédit
- income : revenu du client
default student balance income
No :9667 No :7056 Min. : 0.0 Min. : 772
Yes: 333 Yes:2944 1st Qu.: 481.7 1st Qu.:21340
Median : 823.6 Median :34553
Mean : 835.4 Mean :33517
3rd Qu.:1166.3 3rd Qu.:43808
Max. :2654.3 Max. :73554 On considère donc ici des variables explicatives quantitatives et qualitatives. Le comportement de ces variables est résumé sur la Figure 10.1.
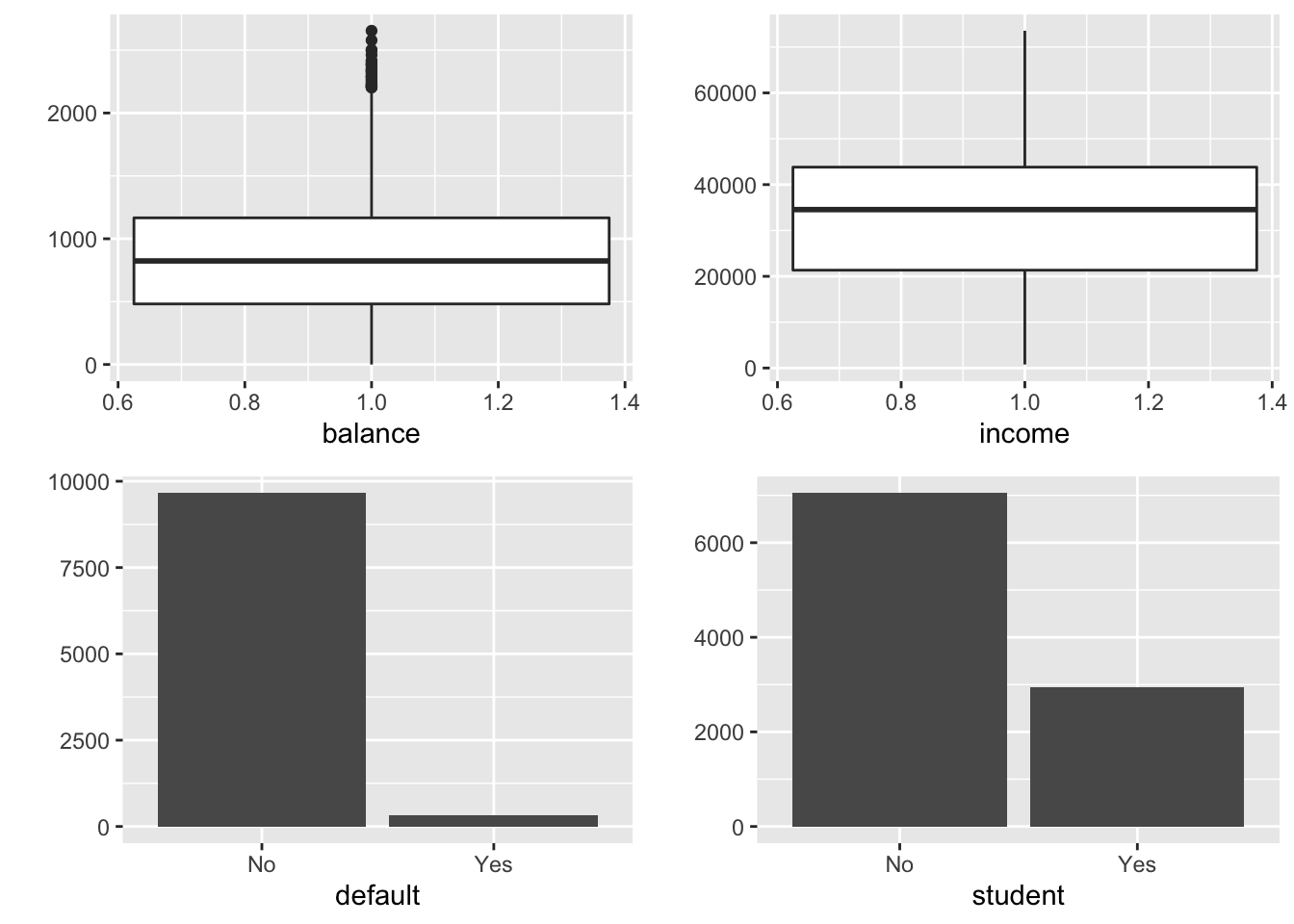
Figure 10.1: Résumé des 4 variables de l’exemple de défaut bancaire.
L’ensemble des méthodes de modélisation disponible pour apporter des réponses à ce type de problème est désigné par le terme de régression logistique.
10.2 Pourquoi des modèles particuliers ?
Dans la suite, on note \(Y=(Y_1,\ldots,Y_n)'\ \in\{0,1\}^n\) le vecteur des réponses, et \(\textbf{x}_i\) le vecteur ligne des variables explicatives considérées pour l’individu \(i\) dans \(\{1\ldots,n\}\).
La variable réponse à expliquer \(Y_i | \textbf{x}_i \sim \mathcal B(\pi(\textbf{x}_i))\) vérifie \[ \mathbb{P}(Y_i=1|\textbf{x}_i) = \pi(\textbf{x}_i). \] L’objectif est de construire un modèle pour reconstituer \(\pi(\textbf{x}_i)=\mathbb{E}[Y_i | \textbf{x}_i]\) en fonction des variables explicatives. Si on utilise le modèle de régression usuel \(Y_i=\textbf{x}_i\theta +\varepsilon_i\) pour une variable binaire, l’e résidu’erreur serait distribuée selon la loi \[ \varepsilon_i=\left\{\begin{array}{ll} 1 - \textbf{x}_i \theta & \textrm{ avec probabilité } \pi(\textbf{x}_i),\\ -\textbf{x}_i \theta & \textrm{ avec probabilité } 1-\pi(\textbf{x}_i). \end{array}\right. \] ce qui est trop éloigné des hypothèses usuelles de normalité des erreurs. De plus, la régression linéaire implique que \(\mathbb{E}[Y_i | \textbf{x}_i]= \textbf{x}_i \theta\). Or \(Y_i | \textbf{x}_i \sim \mathcal B(\pi(\textbf{x}_i))\) donc \(\pi(\textbf{x}_i)=\textbf{x}_i \theta\). Cependant, rien n’indique que \(\textbf{x}_i \theta\in[0,1]\).
Les méthodes proposées partent du principe que le phénomène étudié est l’observation de \(Y_i\) (binaire), qui est la manifestation visible d’une variable \(Z_i\) latente (non observée) continue : \(Y_i = \mathbb{1}_{Z_i >0}\). On considère un modèle linéaire entre \(Z_i\) et \(\textbf{x}_i\) : \[ Z_i = \textbf{x}_i \theta + \varepsilon_i. \] On peut alors remarquer que \[ \pi(\textbf{x}_i) = \mathbb{P}(Y_i=1 | \textbf{x}_i ) = \mathbb{P}(Z_i>0|\textbf{x}_i) = \mathbb{P}(-\varepsilon_i < \textbf{x}_i \theta) = F(\textbf{x}_i \theta), \] où \(F\) est la fonction de répartition de \(-\varepsilon_i\), qui correspond à l’inverse de la fonction de lien \(g\).
Le choix du modèle porte donc sur le choix de cette fonction de répartition \(F\) ou de façon équivalente à la fonction de lien \(g\). Dans le cadre binaire, les fonctions les plus usuellement utilisées sont (Figure 10.2) :
la fonction logistique: \[ F(u)=\frac{e^u}{1+e^u} \quad \Longleftrightarrow \quad g(\pi) = \ln\left(\frac{\pi}{1-\pi}\right)=\textrm{logit}(\pi). \] Cette fonction est bien adaptée à la modélisation de probabilité car elle prend ses valeurs dans \([0,1]\). Dans ce cas, on parle de modèle logistique.
la fonction probit :
\(F\) est la fonction de répartition de la loi \(\mathcal N(0,1)\) et donc \(g=F^{-1}\) est la fonction probit. Dans ce cas, on parle de modèle probit.
- la fonction Gompit ou log-log : \(F\) est la fonction de répartition de la loi de Gompertz \[ F(u) = 1 - \exp\left(-e^{u}\right) \quad \Longleftrightarrow \quad g(\pi) =\ln[-\ln(1-\pi)], \] mais cette fonction est dissymétrique. Dans ce cas, on parle de modèle log-log.
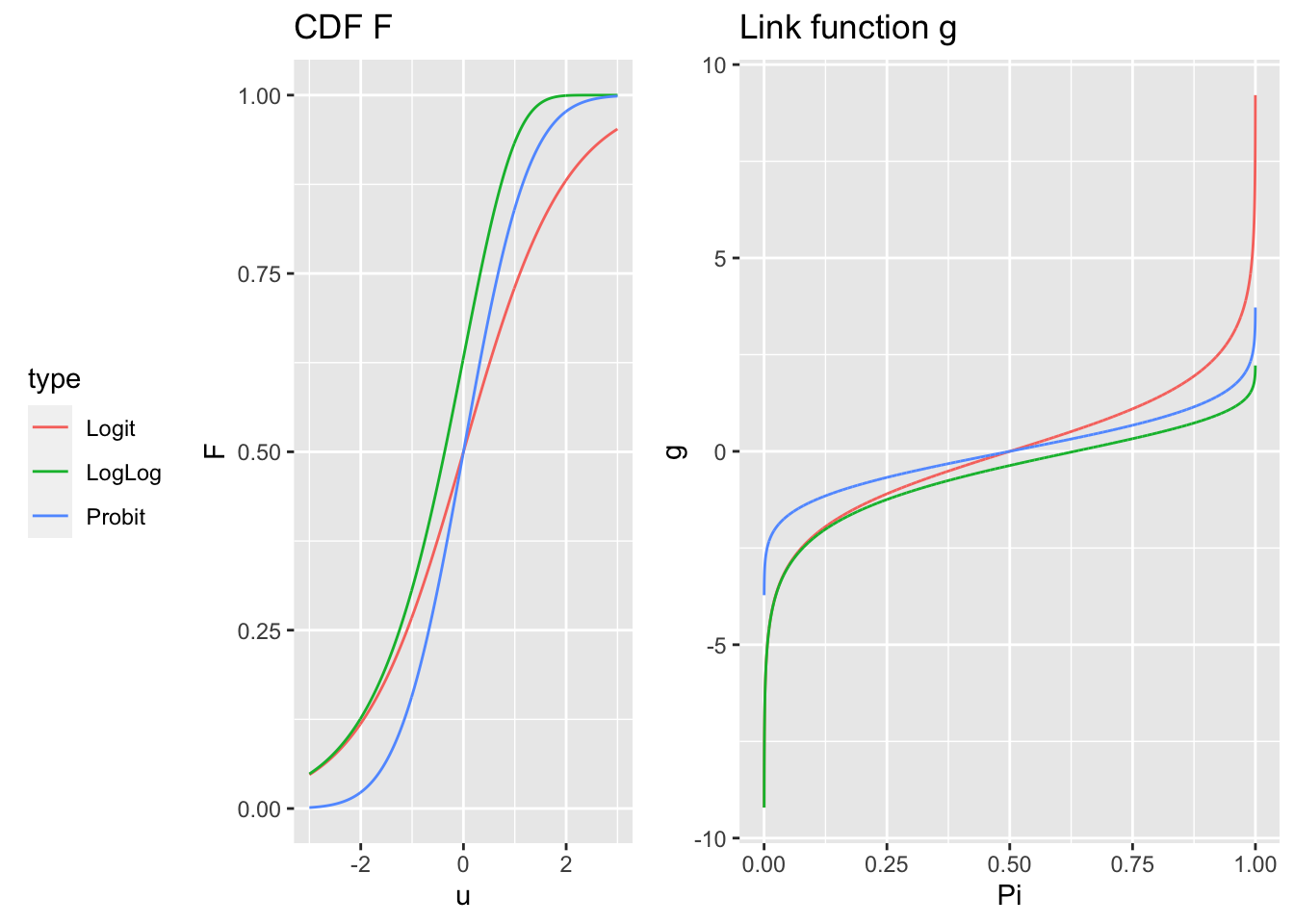
Figure 10.2: Comparaison des fonctions de répartition (à gauche) et des fonctions de lien g (à droite).
10.3 Odds et odds ratio
Il est souvent difficile d’interpréter directement les coefficients \(\theta\), l’interprétation se fait plutôt via les odds ratio. Ces odds ratio servent à mesurer l’effet d’une variable quantitative ou le contraste entre les effets d’une variable qualitative. L’idée générale est de raisonner en termes de probabilités ou de rapport de “chances” (odds).
Definition 10.1 L’odds (chance) pour un individu \({\bf x}\) d’obtenir la réponse \(Y=1\) est défini par : \[ \textrm{odds}({\bf x})= \frac{\pi({\bf x})}{1-\pi({\bf x})}, \quad \textrm{ avec } \pi({\bf x})=\mathbb{P}(Y=1|{\bf x}). \]
L’odds ratio (rapport de chances) entre deux individus \({\bf x}\) et \(\tilde {\bf x}\) est \[ \textrm{OR}({\bf x},\tilde {\bf x}) = \frac{\textrm{odds}({\bf x})}{\textrm{odds}(\tilde {\bf x})}. \]
Example 10.2 Si un joueur \({\bf x}\) a une probabilité \(\pi({\bf x}) = 1/4 = 0.25\) de gagner à un jeu, l’odds de succès vaut \(0.25/0.75 = 1/3\). On dira que les chances de succès sont de 1 contre 3. Remarquons que l’odds d’échec est de \(0.75/0.25 = 3\) et on dira que les chances d’échec sont de 3 contre 1.
Les odds ratio peuvent être utilisés de plusieurs manières :
Comparaison de probabilités de succès entre deux individus : \[ \left\{\begin{array}{r c l} \textrm{OR}({\bf x},\tilde {\bf x}) >1 &\Leftrightarrow & \pi({\bf x}) > \pi(\tilde {\bf x})\\ \textrm{OR}({\bf x},\tilde {\bf x}) =1 &\Leftrightarrow & \pi({\bf x}) = \pi(\tilde {\bf x})\\ \textrm{OR}({\bf x},\tilde {\bf x}) < 1 &\Leftrightarrow & \pi({\bf x}) < \pi(\tilde {\bf x})\\ \end{array} \right. \]
Mesure de l’impact d’une variable : pour le modèle logistique avec intercept, \[ \textrm{logit}[\pi({\bf x})] = \theta_0 + \theta_1 x^{(1)} + \ldots + \theta_p x^{(p)}, \] il est facile de vérifier que \[ \textrm{OR}({\bf x},\tilde {\bf x}) = \prod_{j=1}^p \exp\left[\theta_j (x^{(j)} - \tilde x^{(j)})\right]. \] Pour mesurer l’influence d’une variable sur l’odds ratio, il suffit de considérer deux individus qui diffèrent uniquement sur la \(j\)ème variable. On obtient alors \[ \textrm{OR}({\bf x},\tilde {\bf x}) = \exp\left[\theta_j (x^{(j)} - \tilde x^{(j)})\right]. \] Ainsi une variation de la \(j\)ème variable d’une unité correspond à un odds ratio \(\exp(\theta_j)\) qui est uniquement fonction du coefficient \(\theta_j\). Le coefficient \(\theta_j\) permet de mesurer l’influence de la \(j\)ème variable sur le rapport \(\pi({\bf x})/[1-\pi({\bf x})]\) lorsque \(x^{(j)}\) varie d’une unité, et ce, indépendamment de la valeur \(x^{(j)}\). Une telle analyse peut se révéler intéressante pour étudier l’influence d’un changement d’état d’une variable qualitative.
Interprétation d’un risque relatif : si \(\pi({\bf x})\) et \(\pi(\tilde {\bf x})\) sont petits par rapport à 1 (ex pour une maladie rare), l’odds ratio peut être approché par \(\pi({\bf x})/\pi(\tilde {\bf x})\). On fait alors une interprétation simple : si \(\textrm{OR}({\bf x},\tilde {\bf x}) = 4\), la réponse \(Y=1\) est 4 fois plus probable en \({\bf x}\) qu’en \(\tilde {\bf x}\).
10.4 Régression logistique simple
Dans cette section, on cherche à expliquer la variable réponse binaire \(Y\) par une seule variable explicative. Nous allons distinguer deux cas : celui où la variable explicative est quantitative et celui où elle est qualitative.
10.4.1 Avec une variable explicative quantitative
Dans notre exemple, nous allons chercher à expliquer la variable default à l’aide de la variable explicative balance. La Figure 10.3 montre qu’il est difficile de modéliser les données brutes mais si on regroupe les clients par classe de valeurs de balance, la liaison entre balance et default devient plus claire. Il apparait que lorsque le montant mensuel d’utilisation de la carte de crédit augmente, la proportion de clients en défaut augmente. Au vu de la forme de la courbe de liaison, une modélisation avec le lien logit semble “naturelle”. On va donc chercher à modéliser l’espérance conditionnelle de \(Y_i\) sachant \(\textbf{x}_i=(1,x_i)\), par \(\mathbb{E}[Y_i|\textbf{x}_i] = \pi_\theta(\textbf{x}_i)\), où \[ \pi_\theta(\textbf{x}_i) = F(\theta_0 + \theta_1 x_i)=\frac{e^{\theta_0 + \theta_1 x_i}}{1+e^{\theta_0 + \theta_1 x_i}} \quad \Longleftrightarrow \quad \ln\left(\frac{\pi_\theta({\bf x_i})}{1-\pi_\theta({\bf x_i})}\right) = \theta_0 + \theta_1 x_i. \]
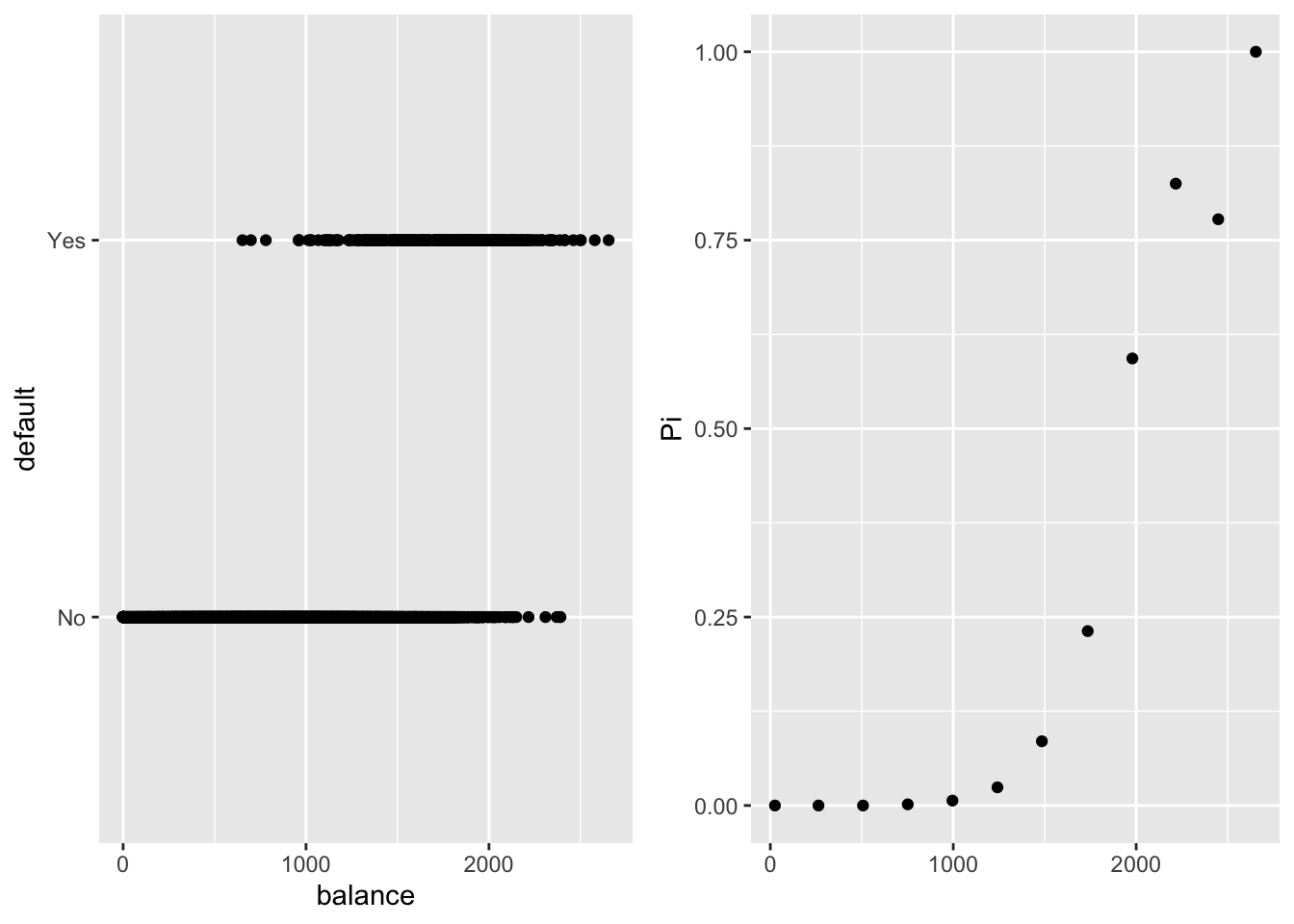
Figure 10.3: A gauche, représentation de default en fonction de balance. A droite, proportion de clients en défaut par classe de valeurs pour balance.
10.4.1.1 Estimation des paramètres
Les paramètres \(\theta=(\theta_0,\theta_1)\) sont estimés par la méthode du maximum de vraisemblance. La vraisemblance des données \(\underline{Y}=(Y_1,\ldots, Y_n)\) est définie par : \[ L(\underline{Y}; \theta) = \prod_{i=1}^n \pi_\theta(\textbf{x}_i)^{Y_i} [1-\pi_\theta(\textbf{x}_i)]^{1-Y_i}, \] et la log-vraisemblance par :
\[\begin{eqnarray*} l(\underline{Y}; \theta) &=& \sum_{i=1}^n \big\{Y_i \ln[\pi_\theta(\textbf{x}_i)] + (1-Y_i)\ln[1-\pi_\theta(\textbf{x}_i)]\big\}\\ &=& \sum_{i=1}^n \big\{Y_i \ln\left[F(\theta_0 + \theta_1 x_i) \right] + (1-Y_i)\ln\left[1-F(\theta_0 + \theta_1 x_i)\right]\big\} \end{eqnarray*}\]
On cherche alors à annuler les dérivées partielles. On commence par remarquer que si \(F(u)=e^u/(1+e^u)\), on a \(F'(u) = F(u) \left[1-F(u)\right]\). D’où
\[\begin{eqnarray*} \frac{\partial l(\underline{Y}; \theta) }{\partial \theta_0} &=& \sum_{i=1}^n \left[Y_i \frac{F'(\theta_0 + \theta_1 x_i)}{F(\theta_0 + \theta_1 x_i)} - (1-Y_i) \frac{F'(\theta_0 + \theta_1 x_i)}{1-F(\theta_0 + \theta_1 x_i)}\right] \\ &=& \sum_{i=1}^n \left[Y_i \left[ 1 - F(\theta_0 + \theta_1 x_i)\right] - (1-Y_i) F(\theta_0 + \theta_1 x_i)\right], \end{eqnarray*}\] et \[\begin{eqnarray*} \frac{\partial l(\underline{Y}; \theta) }{\partial \theta_1} &=& \sum_{i=1}^n \left[Y_i x_i \frac{F'(\theta_0 + \theta_1 x_i)}{F(\theta_0 + \theta_1 x_i)} - (1-Y_i) x_i \frac{F'(\theta_0 + \theta_1 x_i)}{1-F(\theta_0 + \theta_1 x_i)}\right] \\ &=& \sum_{i=1}^n \left[x_i \left[ Y_i - F(\theta_0 + \theta_1 x_i)\right]\right]. \end{eqnarray*}\]
On obtient donc le système suivant : \[ \left\{\begin{array}{l} \sum_{i=1}^n \left[Y_i - F(\theta_0 + \theta_1 x_i)\right] = 0 \\ \sum_{i=1}^n x_i \left[ Y_i - F(\theta_0 + \theta_1 x_i) \right]= 0 \end{array}\right. \quad\Longleftrightarrow\quad \left\{\begin{array}{l} \sum_{i=1}^n \left[Y_i - \pi_\theta(\textbf{x}_i)\right]= 0 \\ \sum_{i=1}^n x_i \left[ Y_i - \pi_\theta(\textbf{x}_i) \right]= 0 \end{array}\right. \]
Pour mettre ensuite en place un algorithme de type Newton-Raphson ou de Fisher-scoring, on a besoin d’évaluer la matrice hessienne ou la matrice d’information de Fisher. Pour cela, on évalue les dérivées secondes : \[ \left\{ \begin{array}{l} \displaystyle\frac{\partial ^2 l(\underline{Y};\theta)}{\partial \theta_0^2} = - \sum_{i=1}^n F'(\theta_0 + \theta_1 x_i) = - \sum_{i=1}^n F(\theta_0 + \theta_1 x_i) [1-F(\theta_0 + \theta_1 x_i)]\\ \\ \displaystyle\frac{\partial ^2 l(\underline{Y};\theta)}{\partial \theta_1^2} = - \sum_{i=1}^n x_i^2 F'(\theta_0 + \theta_1 x_i) = - \sum_{i=1}^n x_i^2 F(\theta_0 + \theta_1 x_i) [1-F(\theta_0 + \theta_1 x_i)]\\ \\ \displaystyle\frac{\partial ^2 l(\underline{Y};\theta)}{\partial \theta_0 \partial \theta_1} = - \sum_{i=1}^n x_i F'(\theta_0 + \theta_1 x_i) = - \sum_{i=1}^n x_i F(\theta_0 + \theta_1 x_i) [1-F(\theta_0 + \theta_1 x_i)] \end{array} \right. \]
La matrice d’information de Fisher vaut alors \[ \mathcal{I}_n(\theta) = \left( \begin{array}{c c} \displaystyle\sum_{i=1}^n \pi_\theta(\textbf{x}_i) (1-\pi_\theta(\textbf{x}_i)) & \displaystyle \sum_{i=1}^n x_i \pi_\theta(\textbf{x}_i) (1-\pi_\theta(\textbf{x}_i)) \\ \displaystyle\sum_{i=1}^n x_i \pi_\theta(\textbf{x}_i) (1-\pi_\theta(\textbf{x}_i)) & \displaystyle \sum_{i=1}^n x_i^2 \pi_\theta(\textbf{x}_i) (1-\pi_\theta(\textbf{x}_i)) \end{array}\right) = \left(X' W X \right), \] avec \[ X=\left(\begin{array}{c c}1 & x_1\\ 1 & x_2 \\ \vdots & \vdots\\ 1 & x_n\end{array}\right) \textrm{ et } W = \mbox{diag}\big[\pi_\theta(\textbf{x}_1) (1-\pi_\theta(\textbf{x}_1))\ ,\ \ldots \ ,\ \pi_\theta(\textbf{x}_n) (1-\pi_\theta(\textbf{x}_n)))\big]. \]
Sur notre exemple, on ajuste ce modèle entre la variable default et la variable balance avec la fonction glm() de R.
Call:
glm(formula = default ~ balance, family = binomial(link = "logit"),
data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.2697 -0.1465 -0.0589 -0.0221 3.7589
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.065e+01 3.612e-01 -29.49 <2e-16 ***
balance 5.499e-03 2.204e-04 24.95 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1596.5 on 9998 degrees of freedom
AIC: 1600.5
Number of Fisher Scoring iterations: 810.4.1.2 Prédiction
Une fois le modèle ajusté, on obtient une estimation pour chaque prédicteur linéaire \(\eta_i=\theta_0 + x_i\theta_1\) par \(\hat \eta_i=\hat \theta_0 + x_i\hat\theta_1\) et pour chaque paramètre \[\hat \pi({\bf x}_i) = F(\hat\eta_i) = F(\hat \theta_0 + \hat \theta_1 x_i) = \pi_{\hat\theta}(\textbf{x}_i).\] En appliquant ensuite la règle de Bayes sur les \(\hat \pi({\bf x}_i)\), on récupère les valeurs ajustées \(\widehat Y_i\) pour les \(Y_i\) : \[ \widehat Y_i = \left\{\begin{array}{l l } 1 & \textrm{ si } \hat \pi({\bf x}_i) > s\\ 0 & \textrm{ sinon}.\end{array}\right. \] où \(s\) est un seuil choisi souvent à \(0.5\) par défaut.
On peut alors comparer par une table de contingence les valeurs prédites par le modèle avec les valeurs observées des réponses. Dans notre exemple, on obtient
hatY
default FALSE TRUE
No 9625 42
Yes 233 100On constate que l’on retrouve assez bien les clients n’ayant pas de défaut, mais mal ceux avec un défaut.
Si on se donne maintenant un nouvel individu décrit par \(\textbf{x}_0=(1,x_0)\) alors le modèle ajusté permet de prédire une proportion \(\hat \pi(\textbf{x}_0)=F(\hat \theta_0 + \hat \theta_1 x_0)\) et une réponse prédite \(\widehat Y_0 = \mathbb{1}_{\hat \pi(\textbf{x}_0) > 0.5}\).
La Figure 10.4 représente l’ajustement des proportions estimées par le modèle logistique et par le modèle probit avec les proportions observées.
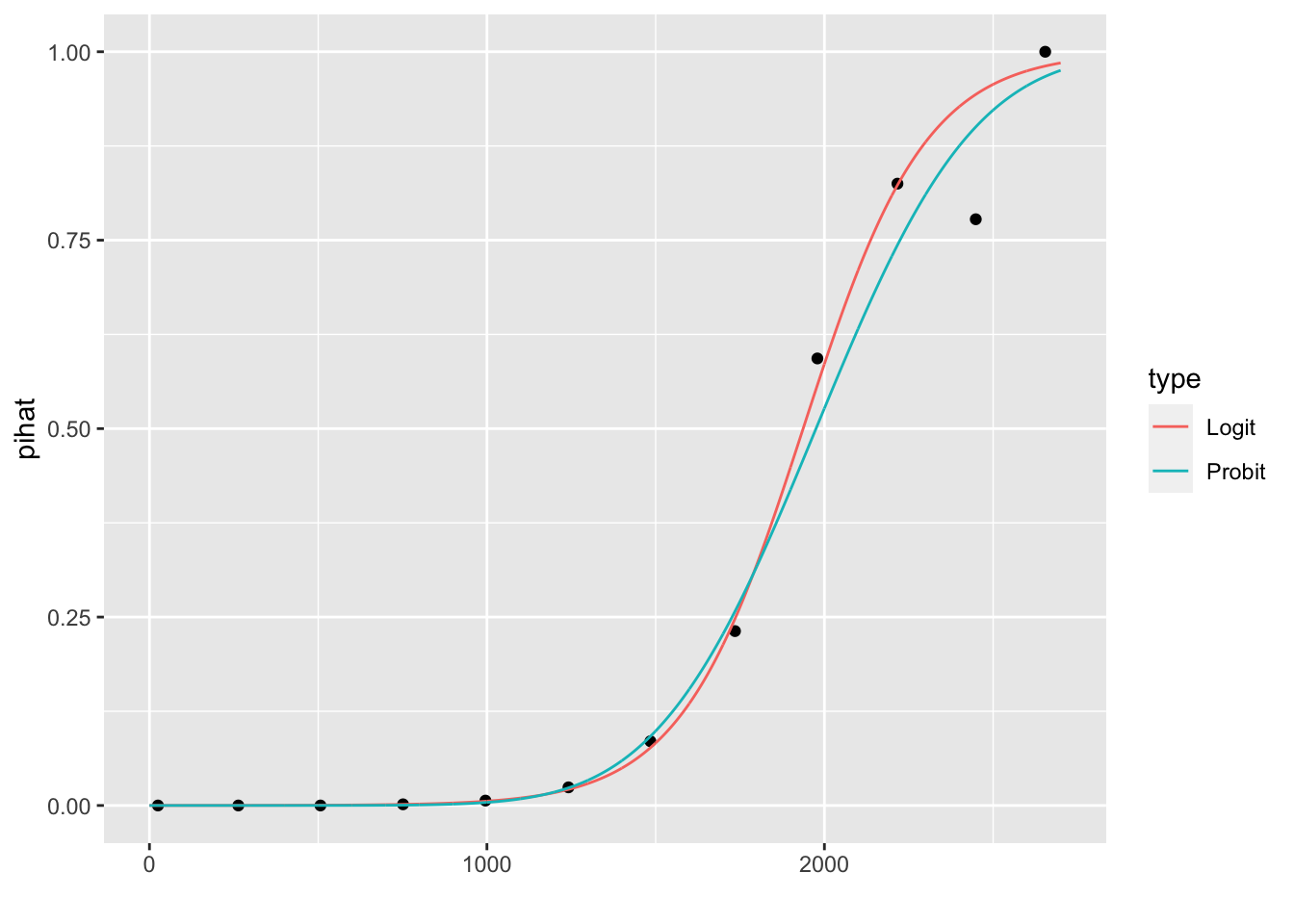
Figure 10.4: Représentation des proportions prédites par le modèle logistique et par le modèle probit.
10.4.1.3 Intervalle de confiance
Pour obtenir un intervalle de confiance pour chaque \(\theta_j\), on peut utiliser la méthode de Wald ou la méthode fondée sur le rapport de vraisemblance présentées en section 9.6. Sous R, le premier est obtenu avec la commande confint.default(), le second avec la commande confint(). Sur notre exemple, on obtient :
2.5 % 97.5 %
(Intercept) -11.383288936 -9.966565064
balance 0.005078926 0.005943365 2.5 % 97.5 %
(Intercept) -11.359186056 -9.943475172
balance 0.005066999 0.00593083510.4.1.4 Test de nullité des paramètres
Si l’on souhaite tester \(\mathcal{H}_0: \theta_j= 0\) contre \(\mathcal{H}_1: \theta_j \neq 0\), on reprend la construction du \(Z\)-test décrite en section 9.5.2. Pour rappel, il suffit de remarquer que sous \(\mathcal{H}_0\), \[ \frac{\hat \theta_j}{\hat \sigma_j} \stackrel{\mathcal L}{\underset{n\to +\infty}{\longrightarrow}} \mathcal{N}(0,1) \] avec \(\hat{\sigma}_j = \sqrt{[\mathcal{I}(\hat{\theta}_{MV})^{-1}]_{jj}}\). On peut alors construire un test asymptotique de niveau \(\alpha\) de zone de rejet \[ \mathcal{R}_\alpha = \left\{ \left| \hat \theta_j / \hat \sigma_j \right| > z_{1-\alpha/2} \right\}, \] où \(z_{1-\alpha/2}\) est le \(1-\alpha/2\). Pour notre exemple, on obtient
Call:
glm(formula = default ~ balance, family = binomial(link = "logit"),
data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.2697 -0.1465 -0.0589 -0.0221 3.7589
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.065e+01 3.612e-01 -29.49 <2e-16 ***
balance 5.499e-03 2.204e-04 24.95 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1596.5 on 9998 degrees of freedom
AIC: 1600.5
Number of Fisher Scoring iterations: 8Les \(p\)-valeurs étant \(<2e^{-16}\), on rejette la nullité pour les deux coefficients.
On peut aussi voir le problème comme un test de sous-modèle et le résoudre avec un test de Wald ou un test du rapport du maximum de vraisemblance. Par exemple, pour tester la nullité de \(\theta_1\) :
Analysis of Deviance Table
Model 1: default ~ 1
Model 2: default ~ balance
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 9999 2920.7
2 9998 1596.5 1 1324.2 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 110.4.2 Avec une variable explicative qualitative
On va chercher ici à expliquer la variable default par rapport à la variable student (binaire). On peut considérer le modèle suivant : \[ \textrm{logit}(\pi({\bf x}_i)) = \ln\left(\frac{\pi({\bf x}_i)}{1-\pi({\bf x}_i)}\right) = \theta_0 + \theta_1 \mathbb{1}_{x_i =1} + \theta_2 \mathbb{1}_{x_i =0}. \] Mais on peut remarquer qu’il est possible d’écrire le modèle également sous la forme \[ \textrm{logit}(\pi({\bf x}_i)) = \ln\left(\frac{\pi({\bf x}_i)}{1-\pi({\bf x}_i)}\right) = (\theta_0 + \theta_2) + (\theta_1 - \theta_2) \mathbb{1}_{x_i =1} + 0\ \mathbb{1}_{x_i =0}. \] On se retrouve comme pour l’analyse de variance avec un modèle non identifiable. Il faut donc imposer une contrainte sur les paramètres pour le rendre identifiable. Par exemple si on suppose que \(\theta_2=0\), le modèle devient \[\textrm{logit}(\pi({\bf x}_i)) = \theta_0 + \theta_1 \mathbb{1}_{x_i=1}.\] Il faut donc adapter l’interprétation des paramètres selon la contrainte considérée.
On peut alors reprendre les mêmes raisonnements et les mêmes calculs que dans la section 10.4.1 pour estimer les paramètres, construire un intervalle de confiance pour chacun des paramètres, tester la nullité de chacun des paramètres, etc.
Dans notre exemple traité sous R, le modèle considéré est celui avec la contrainte \(\theta_2=0\) :
student
default No Yes
No 6850 2817
Yes 206 127
Call:
glm(formula = default ~ student, family = binomial, data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.2970 -0.2970 -0.2434 -0.2434 2.6585
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.50413 0.07071 -49.55 < 2e-16 ***
studentYes 0.40489 0.11502 3.52 0.000431 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 2908.7 on 9998 degrees of freedom
AIC: 2912.7
Number of Fisher Scoring iterations: 6Pour l’interprétation des paramètres, on s’appuie sur les odds et odds ratio. On a que \(odds(x_i=0)=e^{\theta_0}\), \(odds(x_i=1)=e^{\theta_0 + \theta_1}\) et \(OR(x_i=1,x_i=0) = e^{\theta_1}\).
new.data=data.frame(student=factor(c("No","Yes")))
inv.logit(predict(glm.student,new.data)) # nécessite la librairie boot 1 2
0.02919501 0.04313859 (Intercept) studentYes sum
0.03007299 1.49913321 0.04508342 :::
Si on n’est pas étudiant, \(\textrm{logit}(\hat \pi) = \hat \theta_0\) donc \(\hat \pi = 0.029\) alors que si l’on est étudiant, \(\textrm{logit}(\hat\pi) = \hat \theta_0 + \hat \theta_1\) d’où \(\hat \pi = 0.043\). Ainsi, \[ \left\{\begin{array}{l} \mbox{odds}(\mbox{"étudiant"}) = 0.045, \\ \mbox{odds}(\mbox{"non étudiant"}) = 0.030, \\ \mbox{OR}(\mbox{"étudiant"},\mbox{"non étudiant"}) = 1.5. \end{array}\right. \] Un étudiant a 1.5 fois plus de chance d’être en défaut qu’une personne non étudiante.
Pour tester la pertinence d’utiliser la variable student, on peut également faire un test de sous-modèle :
Analysis of Deviance Table
Model 1: default ~ 1
Model 2: default ~ student
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 9999 2920.7
2 9998 2908.7 1 11.967 0.0005416 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On en déduit que le modèle prenant en compte la variable student est meilleur que le modèle nul.
10.5 Régression logistique multiple
Dans cette section, nous allons considérer le cas plus général où l’on souhaite expliquer la variable réponse binaire \(Y\) par rapport à \(p\) régresseurs \(x^{(1)},\ldots,x^{(p)}\). Dans l’exemple, on a \(p=3\) régresseurs, une variable qualitative (student = \(x^{(1)}\)) et deux variables quantitatives (balance = \(x^{(2)}\), income=\(x^{(3)}\)). Nous allons aborder plusieurs questions au travers de l’étude de cet exemple.
10.5.1 Modèle sans interaction
Dans un premier temps, on considère le modèle complet sans interaction suivant : \[ \textrm{logit}(\pi({\bf x}_i)) = \theta_0 + \theta_1\ \mathbb{1}_{x^{(1)}_i = 1} + \theta_2\ x^{(2)}_i + \theta_3\ x^{(3)}_i. \] Le code suivant sous R permet d’ajuster ce modèle sans interaction :
Call:
glm(formula = default ~ ., family = binomial(link = "logit"),
data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4691 -0.1418 -0.0557 -0.0203 3.7383
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.087e+01 4.923e-01 -22.080 < 2e-16 ***
studentYes -6.468e-01 2.363e-01 -2.738 0.00619 **
balance 5.737e-03 2.319e-04 24.738 < 2e-16 ***
income 3.033e-06 8.203e-06 0.370 0.71152
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1571.5 on 9996 degrees of freedom
AIC: 1579.5
Number of Fisher Scoring iterations: 8On obtient les estimations pour chacun des paramètres. On constate que si on teste la nullité individuellement de chaque paramètre par le test de Wald ou le \(Z\)-test, on rejette la nullité de \(\theta_0, \theta_1, \theta_2\) et on accepte la nullité de \(\theta_3\).
10.5.1.1 Test de nullité de plusieurs coefficients simultanément.
Testons la nullité de \(\theta_2\) et \(\theta_3\) simultanément. On peut le voir comme un test de sous-modèle comparant le modèle complet sans interaction avec le modèle (introduit en section 10.4.2) \[ \textrm{logit}(\pi({\bf x}_i)) = \theta_0 + \theta_1 \mathbb{1}_{x^{(1)}_i = 1} . \]
Analysis of Deviance Table
Model 1: default ~ student
Model 2: default ~ student + balance + income
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 9998 2908.7
2 9996 1571.5 2 1337.1 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On rejette la nullité simultanée de ces deux paramètres. On peut aussi voir l’hypothèse nulle sous la forme \[ \mathcal{H}_0: C\theta = 0_2 \textrm{ avec } C=\left(\begin{array}{c c c c} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right). \]
On peut alors reprendre la construction du test de Wald présenté en section 9.5.1.2. On contrôle ici numériquement les quantités considérées dans ce test pour notre exemple
hattheta <- glm.additif$coefficients
hatpi <- glm.additif$fitted.values
W <- diag(hatpi*(1-hatpi))
X <- cbind(rep(1,10000),student,balance,income)
In <- t(X) %*% W %*% X
C <- matrix(c(0,0,1,0,0,0,0,1),nrow=4)
t(t(C)%*%hattheta) %*% solve(t(C)%*%solve(In)%*%C) %*% (t(C)%*%hattheta) > qchisq(0.95,df=2) [,1]
[1,] TRUEOn rejette l’hypothèse nulle.
10.5.1.2 Sélection de variables
Plus généralement, on peut envisager une procédure de sélection de variables. On choisit ici de faire une sélection de variable descendante avec le critère AIC :
Start: AIC=1579.54
default ~ student + balance + income
Df Deviance AIC
- income 1 1571.7 1577.7
<none> 1571.5 1579.5
- student 1 1579.0 1585.0
- balance 1 2907.5 2913.5
Step: AIC=1577.68
default ~ student + balance
Df Deviance AIC
<none> 1571.7 1577.7
- student 1 1596.5 1600.5
- balance 1 2908.7 2912.7On peut également utiliser la fonction stepAIC() de la librairie MASS avec le critère AIC (option “p=2”) ou BIC (option "p=log(n))
library(MASS)
stepAIC(glm.additif, direction=c("backward"),p=2) # AIC
stepAIC(glm.additif, direction=c("backward"),p=log(nrow(Default))) # BICPour les trois procédures, le modèle sélectionné est également celui sans la variable income.
10.5.2 Modèle avec interactions
On va considérer ici le modèle complet avec toutes les interactions (d’ordre 2) entre variables et on met en place une procédure de sélection de variables pour déterminer un modèle plus simple pour expliquer la variable réponse default. Le modèle s’écrit : \[ \textrm{logit}(\pi({\bf x}_i)) = \theta_0 + \theta_2 x^{(2)}_i + \theta_3 x^{(3)}_i + \theta_{23} x^{(2)}_i x^{(3)}_i+ (\beta_1 + \beta_2 x^{(2)}_i + \beta_3 x^{(3)}_i ) \mathbb{1}_{x^{(1)}_i = 1}. \]
On commence par ajuster le modèle complet avec interactions avec le code suivant :
Call:
glm(formula = default ~ .^2, family = "binomial", data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4848 -0.1417 -0.0554 -0.0202 3.7579
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.104e+01 1.866e+00 -5.914 3.33e-09 ***
studentYes -5.201e-01 1.344e+00 -0.387 0.699
balance 5.882e-03 1.180e-03 4.983 6.27e-07 ***
income 4.050e-06 4.459e-05 0.091 0.928
studentYes:balance -2.551e-04 7.905e-04 -0.323 0.747
studentYes:income 1.447e-05 2.779e-05 0.521 0.602
balance:income -1.579e-09 2.815e-08 -0.056 0.955
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1571.1 on 9993 degrees of freedom
AIC: 1585.1
Number of Fisher Scoring iterations: 8On peut remarquer que le test de nullité de chaque paramètre individuellement est accepté pour plusieurs des paramètres. On poursuit notre étude en cherchant à simplifier le modèle par sélection de variable. On applique une procédure de sélection de variable avec le critère AIC :
Start: AIC=1585.07
default ~ (student + balance + income)^2
Df Deviance AIC
- balance:income 1 1571.1 1583.1
- student:balance 1 1571.2 1583.2
- student:income 1 1571.3 1583.3
<none> 1571.1 1585.1
Step: AIC=1583.07
default ~ student + balance + income + student:balance + student:income
Df Deviance AIC
- student:balance 1 1571.3 1581.3
- student:income 1 1571.3 1581.3
<none> 1571.1 1583.1
Step: AIC=1581.28
default ~ student + balance + income + student:income
Df Deviance AIC
- student:income 1 1571.5 1579.5
<none> 1571.3 1581.3
- balance 1 2907.3 2915.3
Step: AIC=1579.54
default ~ student + balance + income
Df Deviance AIC
- income 1 1571.7 1577.7
<none> 1571.5 1579.5
- student 1 1579.0 1585.0
- balance 1 2907.5 2913.5
Step: AIC=1577.68
default ~ student + balance
Df Deviance AIC
<none> 1571.7 1577.7
- student 1 1596.5 1600.5
- balance 1 2908.7 2912.7
Call: glm(formula = default ~ student + balance, family = "binomial",
data = Default)
Coefficients:
(Intercept) studentYes balance
-10.749496 -0.714878 0.005738
Degrees of Freedom: 9999 Total (i.e. Null); 9997 Residual
Null Deviance: 2921
Residual Deviance: 1572 AIC: 1578Une fois encore c’est le modèle additif avec seulement les variables student et balance qui est retenu.
10.5.3 Etude complémentaire du modèle retenu
On commence par ajuster le modèle retenu \[ \textrm{logit}(\pi({\bf x}_i)) = \theta_0 + \theta_1 \mathbb{1}_{x^{(1)}_i = 1} + \theta_2 x^{(2)}_i \] à l’aide du code suivant
Call:
glm(formula = default ~ student + balance, family = binomial,
data = Default)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4578 -0.1422 -0.0559 -0.0203 3.7435
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.075e+01 3.692e-01 -29.116 < 2e-16 ***
studentYes -7.149e-01 1.475e-01 -4.846 1.26e-06 ***
balance 5.738e-03 2.318e-04 24.750 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1571.7 on 9997 degrees of freedom
AIC: 1577.7
Number of Fisher Scoring iterations: 8On peut vérifier graphiquement la non-interaction entre les variables student et balance.
Sur la Figure 10.5, on constate que les droites représentant \(\textrm{logit}(\pi_\theta(\cdot))\) en fonction de la variable balance en distinguant selon la valeur de la variable student sont parallèles.
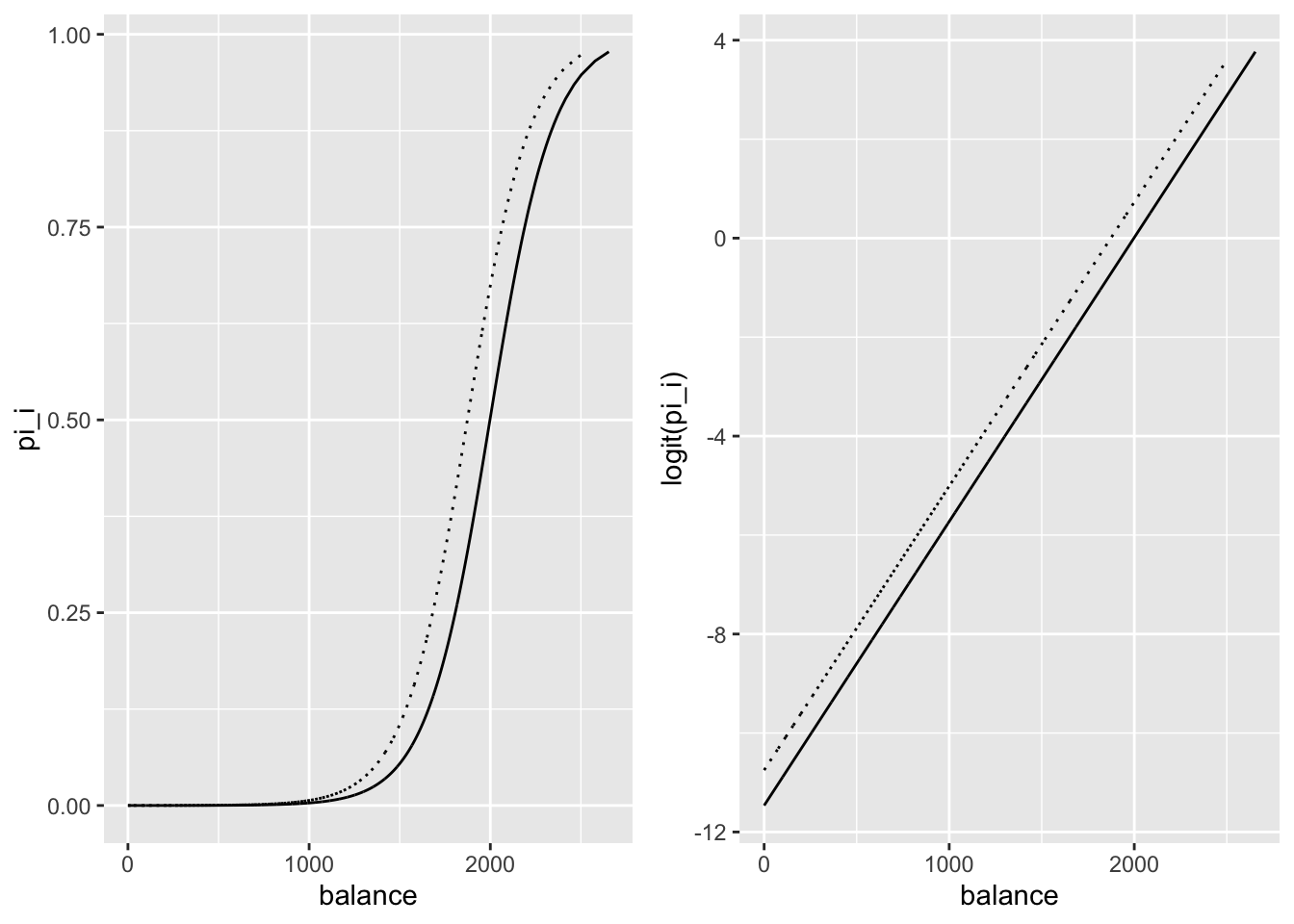
Figure 10.5: Tracé de pi estimé (à gauche) et de la fonction logit appmliquée à pi estimé (à droite) en fonction de la variable balance en distinguant selon la valeur de la variable student (student = 1 en ligne pleine et = 0 en pointillé)
Afin de comparer les valeurs de la variable réponse et les valeurs prédites par le modèle, on forme la table de contingence :
default FALSE TRUE
No 9628 39
Yes 228 105On constate que l’on retrouve assez bien les clients sans défaut sur leur dette, par contre la détection des clients étant en défaut sur leur dette sont très mal prédits.
Concernant les résidus du modèle ajusté, on peut calculer les différents résidus introduits dans le chapitre général (section 9.8).
library(boot)
#residus y_i - \hat\mu_i
res<-residuals(glm.final,type="response")
#residus de deviance
res_dev<-residuals(glm.final)
#residus de Pearson
res_pear<-residuals(glm.final,type="pearson")
#residus de deviance standardisés
res_dev_stand<-rstandard(glm.final)
res_dev_stand<-glm.diag(glm.final)$rd
# residus de Pearson standardisés
H<-influence(glm.final)$hat
res_pear_stand<-res_pear/sqrt(1-H)
res_pear_stand<-glm.diag(glm.final)$rp
# residus de Jackknife
res_Jackknife<-glm.diag(glm.final)$res10.6 Quelques codes avec python
import pandas as pd
import numpy as np
import statsmodels.api as sm
Defaultpy=r.Default
y=Defaultpy["default"].cat.codes
x=Defaultpy["balance"]
x_stat = sm.add_constant(x)
modelbalance = sm.Logit(y, x_stat).fit()Optimization terminated successfully.
Current function value: 0.079823
Iterations 10<class 'statsmodels.iolib.summary.Summary'>
"""
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 10000
Model: Logit Df Residuals: 9998
Method: MLE Df Model: 1
Date: Jeu, 28 oct 2021 Pseudo R-squ.: 0.4534
Time: 12:20:44 Log-Likelihood: -798.23
converged: True LL-Null: -1460.3
Covariance Type: nonrobust LLR p-value: 6.233e-290
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -10.6513 0.361 -29.491 0.000 -11.359 -9.943
balance 0.0055 0.000 24.952 0.000 0.005 0.006
==============================================================================
Possibly complete quasi-separation: A fraction 0.13 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.
""" 0 1
const -11.359208 -9.943453
balance 0.005067 0.005931<class 'statsmodels.iolib.summary.Summary'>
"""
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 10000
Model: Logit Df Residuals: 9998
Method: MLE Df Model: 1
Date: Jeu, 28 oct 2021 Pseudo R-squ.: 0.4534
Time: 12:20:46 Log-Likelihood: -798.23
converged: True LL-Null: -1460.3
Covariance Type: nonrobust LLR p-value: 6.233e-290
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -10.6513 0.361 -29.491 0.000 -11.359 -9.943
balance 0.0055 0.000 24.952 0.000 0.005 0.006
==============================================================================
Possibly complete quasi-separation: A fraction 0.13 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.
"""from scipy.stats import chi2
LR_stat = (-2)* (modelbalance.llnull - modelbalance.llf);
df = 1
pvalue = 1 - chi2(df).cdf(LR_stat);
print(LR_stat)1324.19802796384720.0y=Defaultpy["default"].cat.codes
x=Defaultpy["student"].cat.codes
x_stat = sm.add_constant(x)
modelstudent = sm.Logit(y, x_stat).fit();Optimization terminated successfully.
Current function value: 0.145434
Iterations 7<class 'statsmodels.iolib.summary.Summary'>
"""
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 10000
Model: Logit Df Residuals: 9998
Method: MLE Df Model: 1
Date: Jeu, 28 oct 2021 Pseudo R-squ.: 0.004097
Time: 12:20:48 Log-Likelihood: -1454.3
converged: True LL-Null: -1460.3
Covariance Type: nonrobust LLR p-value: 0.0005416
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -3.5041 0.071 -49.554 0.000 -3.643 -3.366
0 0.4049 0.115 3.520 0.000 0.179 0.630
==============================================================================
"""Defaultpy=r.DefaultBIS
y=Defaultpy["default"]
x=Defaultpy[Defaultpy.columns.drop("default")]
x_stat = sm.add_constant(x)
modeladditif = sm.Logit(y, x_stat).fit()Optimization terminated successfully.
Current function value: 0.078577
Iterations 10<class 'statsmodels.iolib.summary.Summary'>
"""
Logit Regression Results
==============================================================================
Dep. Variable: default No. Observations: 10000
Model: Logit Df Residuals: 9996
Method: MLE Df Model: 3
Date: Jeu, 28 oct 2021 Pseudo R-squ.: 0.4619
Time: 12:20:50 Log-Likelihood: -785.77
converged: True LL-Null: -1460.3
Covariance Type: nonrobust LLR p-value: 3.257e-292
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -10.8690 0.492 -22.079 0.000 -11.834 -9.904
student -0.6468 0.236 -2.738 0.006 -1.110 -0.184
balance 0.0057 0.000 24.737 0.000 0.005 0.006
income 3.033e-06 8.2e-06 0.370 0.712 -1.3e-05 1.91e-05
==============================================================================
Possibly complete quasi-separation: A fraction 0.15 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.
"""10.7 Régression polytomique
On souhaite étendre la régression logistique au cas de l’étude d’une variable réponse qualitative \(Y\) pouvant prendre \(M\) modalités \(u_1,\ldots,u_M\) avec \(M>2\). On note \(x^{(1)},\ldots,x^{(p)}\) les variables explicatives.
10.7.1 Régression multinomiale ou polytomique non-ordonnée
Dans cette section, on considère l’exemple suivant.
Example 10.3 On considère \(n=735\) clients. On souhaite étudier pour un produit le choix du client entre la marque à petit prix, la marque de l’enseigne ou la marque de référence du marché. On souhaite savoir si l’âge et/ou le genre du client a une influence sur son choix.
D <- read.table("Data/MarqueSexe.csv",header=T,sep=";")
D[,"femme"] <- as.factor(D[,"femme"])
D[,1] <- factor(D[,1], levels =c("Reference","Enseigne","PetitPrix"))
summary(D) brand femme age
Reference:221 0:269 Min. :24.0
Enseigne :307 1:466 1st Qu.:32.0
PetitPrix:207 Median :32.0
Mean :32.9
3rd Qu.:34.0
Max. :38.0 La variable réponse \(Y\) est ici nominale, c’est-à-dire que les \(M\) modalités n’ont pas de lien hiérarchique, pas d’ordre. On parle alors de régression multinomiale (ou polytomique non-ordonnée). Comme dans le cas binaire, on cherche à modéliser \[ \pi_m(\textbf{x})=\mathbb{P}(Y=u_m|\textbf{x}),\, \forall m\in\{1,\ldots,M\}. \] Comme \(\sum_{m=1}^M \pi_m(\textbf{x})=1\), il suffit de modéliser \((M-1)\) des \(\pi_m(\textbf{x})\). La catégorie de référence s’impose souvent par le contexte d’étude : les non-malades contre les différents types de maladie; le produit phare du marché contre les produits outsiders, etc. Dans notre exemple, la modalité “Référence” sera considérée comme la modalité de référence.
Dans la suite, nous considérons la première modalité comme référence. On définit alors le modèle de régression multinomiale par \[ \ln\left[\frac{\pi_m(\textbf{x})}{\pi_1(\textbf{x})}\right] = \theta_0^{(m)} + \theta_1^{(m)} x^{(1)} + \ldots + \theta_p^{(m)} x^{(p)} = \textbf{x} \theta^{(m)},\, \forall m\in\{2,\ldots,M\} \] avec \(\textbf{x}=(1,x^{(1)},\ldots,x^{(p)})\) et \(\theta^{(m)} = (\theta_0^{(m)},\theta_1^{(m)} ,\ldots,\theta_p^{(m)})'\) paramètres inconnus. Ceci revient à \[ \pi_m({\bf x})= \frac{\exp(\textbf{x}\theta^{(m)})}{ 1 + \sum_{m'=2}^M \exp(\textbf{x} \theta^{(m')})}. \] On peut remarquer que pour \(M=2\), \(u_1=0\) et \(u_2=1\), on retrouve le modèle de régression logistique.
Pour estimer les paramètres \(\theta^{(m)}\) pour \(m\in\{2,\ldots,M\}\), on cherche à maximiser la vraisemblance du modèle \[ L(\underline{Y}|\theta) = \prod_{i=1}^n \prod_{m=1}^M \pi_{m}(\textbf{x}_i)^{\mathbb{1}_{Y_i=u_m}}. \] On retrouve la vraisemblance de \(n\) lois multinomiales de paramètres \((1,(\pi_1(\textbf{x}_i),\ldots,\pi_M(\textbf{x}_i))\) pour \(1\leq i\leq n\).
Comme pour le cas binaire, il n’y a pas de solutions explicites pour les estimateurs, on utilise donc des méthodes numériques pour les évaluer. A partir des estimateurs \(\hat\theta^{(1)},\ldots,\hat\theta^{(M)}\), on en déduit un estimateur pour chaque \(\pi_m({\bf x})\) : \[ \left\{\begin{array}{l} \displaystyle \hat \pi_m(\textbf{x}) = \frac{\exp(\textbf{x} \hat\theta^{(m)})}{ 1 + \sum_{m'=2}^M \exp(\textbf{x} \hat\theta^{(m')})}, \forall m\in\{2,\ldots,M\} \\ \displaystyle \hat \pi_{1}(\textbf{x}) = 1 - \sum_{m=2}^M \hat \pi_m(\textbf{x}). \end{array}\right. \]
On peut ensuite s’intéresser à la prédiction. Sachant qu’un individu prend les valeurs \(\textbf{x}_0=(1,x_0^{(1)},\ldots, x_0^{(p)})\) on peut faire de la prédiction :
- sur la probabilité que \(Y_0=u_m\) pour \(m\in\{1,\ldots,M\}\) : \(\hat \pi_m(\textbf{x}_0)\).
- sur la modalité de \(Y\) la plus probable pour \(\textbf{x}_0\) \[ \hat Y_0 = u_{\hat m_0} \textrm{ avec } \hat m_0 = \underset{m\in\{1,\ldots,M\}}{\mbox{argmax}} \hat \pi_m(\textbf{x}_0). \]
Sous des conditions similaires au cas binaire, on récupère les mêmes résultats sur le comportement asymptotique des estimateurs. On peut alors utiliser de la même façon les tests de Wald, du rapport de maximum de vraisemblance, etc.
Pour interpréter les paramètres, on peut utiliser les odds ratio. On définit l’odds d’une modalité \(m_1\) contre une modalité \(m_2\) par \[ \textrm{odds}(Y=u_{m_1} \mbox{vs }Y=u_{m_2} ; {\bf x}) = \frac{\mathbb{P}(Y=u_{m_1} | {\bf x}) }{\mathbb{P}(Y=u_{m_2} | {\bf x}) } = \frac{\pi_{m_1}({\bf x})}{\pi_{m_2}({\bf x})} = \exp[{\bf x} (\theta^{(m_1)} - \theta^{(m_2)})]. \] Pour deux individus \(x\) et \(\tilde{x}\), on définit alors l’odds ratio par \[\begin{eqnarray*} \textrm{OR}(Y=u_{m_1} \mbox{vs }Y=u_{m_2} ; {\bf x},\tilde{\bf x}) &=& \frac{\textrm{odds}(Y=u_{m_1} \mbox{vs }Y=u_{m_2} ; {\bf x})}{\textrm{odds}(Y=u_{m_1} \mbox{vs }Y=u_{m_2} ; \tilde{\bf x})} \\ &=& \exp[({\bf x} - \tilde{\bf x}) (\theta^{(m_1)} - \theta^{(m_2)})]. \end{eqnarray*}\] Ainsi si les deux individus \({\bf x}\) et \(\tilde{\bf x}\) ne diffèrent que d’une unité pour la variable \(j\), on a \[ \textrm{OR}(Y=u_{m_1} \mbox{vs }Y=u_{m_2} ; {\bf x},\tilde{\bf x}) = \exp[\theta_j^{(m_1)} - \theta_j^{(m_2)}]. \]
En pratique, on peut utiliser les fonctions multinom() ou vglm() des librairires nnet et VGAM pour ajuster un modèle de régression polytomique non-ordonnée sous R.
Sur notre exemple, une régression multinomiale est mise en oeuvre avec la fonction multinom() :
# weights: 12 (6 variable)
initial value 807.480032
iter 10 value 702.971567
final value 702.970704
convergedOn affiche les estimations obtenues pour les paramètres \(\theta^{(m)}\) pour \(m=2,3\) :
Call:
multinom(formula = brand ~ femme + age, data = D, Hess = T)
Coefficients:
(Intercept) femme1 age
Enseigne 10.94688 0.05798805 -0.3177081
PetitPrix 22.72150 -0.46576724 -0.6859142
Std. Errors:
(Intercept) femme1 age
Enseigne 1.493166 0.1964261 0.04400704
PetitPrix 2.058030 0.2260886 0.06262666
Residual Deviance: 1405.941
AIC: 1417.941 Par exemple, on a \(\ln [\pi_{\tt{\tiny petit prix}} / \pi_{\tt{\tiny Reference}} ] = 22.72 - 0.47 \mathbb{1}_{Femme=1} -0.69 {\tt age}\). Les femmes ont moins confiance dans la marque petit prix par rapport à la marque de référence et plus l’âge augmente, moins le client fait le choix de la marque petit prix par rapport à la marque de référence.
On peut alors calculer les estimations pour les \(\pi_m(\textbf{x}_i)\). Pour chaque individu du jeu de données, on récupère les probabilités avec regMarq$fitted.values :
Reference Enseigne PetitPrix
1 0.001812569 0.05023105 0.9479564
2 0.006741608 0.09896542 0.8942930
3 0.006741608 0.09896542 0.8942930
4 0.018431742 0.20868509 0.7728832
5 0.018431742 0.20868509 0.7728832
6 0.012740144 0.13611798 0.8511419Ainsi pour le premier client, il fera plutôt le choix de la marque petit prix.
On obtient les prédictions avec
apply(regMarq$fitted.values,1,which.max)
ou directement avec la commande
pr = predict(regMarq, D). La matrice de confusion vaut alors
pr
Reference Enseigne PetitPrix
Reference 110 101 10
Enseigne 51 238 18
PetitPrix 13 136 58On peut déterminer un intervalle de confiance pour chacun des paramètres avec la commande :
, , Enseigne
2.5 % 97.5 %
(Intercept) 8.0203294 13.8734340
femme1 -0.3270001 0.4429762
age -0.4039603 -0.2314558
, , PetitPrix
2.5 % 97.5 %
(Intercept) 18.6878390 26.75516759
femme1 -0.9088928 -0.02264168
age -0.8086602 -0.56316817Pour tester la nullité de chaque coefficient \(\theta_j^{(m)}=0\) contre \(\theta_j^{(m)}\neq 0\), on fait un test de Wald (ou Z-test). On obtient les \(p\)-valeurs de chaque test avec les commandes suivantes :
z = summary(regMarq)$coeff / summary(regMarq)$standard.errors
pvaleur = 2 * (1 - pnorm(abs(z), 0, 1))
pvaleur (Intercept) femme1 age
Enseigne 2.278178e-13 0.76782920 5.218048e-13
PetitPrix 0.000000e+00 0.03938811 0.000000e+00On peut aussi utiliser la fonction coeftest() de la librairie AER :
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
Enseigne:(Intercept) 10.946882 1.493166 7.3313 2.279e-13 ***
Enseigne:femme1 0.057988 0.196426 0.2952 0.76783
Enseigne:age -0.317708 0.044007 -7.2195 5.219e-13 ***
PetitPrix:(Intercept) 22.721503 2.058030 11.0404 < 2.2e-16 ***
PetitPrix:femme1 -0.465767 0.226089 -2.0601 0.03939 *
PetitPrix:age -0.685914 0.062627 -10.9524 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On peut remarquer que les variances de chaque coefficient sont données sur la diagonale de l’inverse de la matrice hessienne. Par exemple, pour “femme-enseigne” on retrouve bien l’écart-type \(0.1964\) :
[1] 0.1964261Pour tester le modèle considéré contre le sous-modèle trivial (seulement l’intercept \(\theta_0^{(m)}\)), on considère le test du rapport de vraisemblance :
# weights: 6 (2 variable)
initial value 807.480032
final value 795.895819
convergedrv = regMarq0$deviance - regMarq$deviance
ddl = regMarq$edf - regMarq0$edf
pvaleur = 1 - pchisq(rv, ddl)
print(c(rv,ddl,pvaleur))[1] 185.8502 4.0000 0.0000La différence des déviances vaut \(185.85\). La statistique de test suit une loi du chi-deux à \([n-(M-1)] - [n-(p+1)(M-1)] = p(M-1) = 4\) degrés de liberté. La \(p\)-valeur étant très faible, on rejette l’hypothèse nulle.
On veut maintenant tester si la variable sexe joue un rôle dans le choix des clients. On va donc tester si $_0 : _1^{(2)} = _1^{(3)} =0 $ contre \(\mathcal{H}_1: \exists m; \theta_1^{(m)}\neq 0\). La statistique du test \((\hat\theta_1^{(2)},\hat\theta_1^{(3)}) \hat \Sigma_1^{-1} (\hat\theta_1^{(2)},\hat\theta_1^{(3)})'\) suit une loi du chi-deux à \(2\) degrés de liberté, où \(\hat \Sigma_1\) est la matrice de variance-covariance pour la variable “femme”. On peut aussi le voir comme un test de sous-modèle avec le test du rapport de vraisemblance.
# weights: 9 (4 variable)
initial value 807.480032
final value 706.796304
convergedrv1 = regMarq1$deviance - regMarq$deviance
ddl = regMarq$edf - regMarq1$edf
pvaleur = 1 - pchisq(rv1, ddl)
print(c(rv1,ddl,pvaleur))[1] 7.65119936 2.00000000 0.02180536# TEST 2
thetafemme <- summary(regMarq)$coeff[,2]
Sigmafemme <- Sigma[c(2,5),c(2,5)]
Wfemme <- thetafemme %*% solve(Sigmafemme) %*% thetafemme
Wfemme > qchisq(0.95,2) # test à 5% [,1]
[1,] TRUEComme la \(p\)-valeur vaut \(0.0218\), on rejette l’absence d’effet de la variable sexe à \(5\%\).
Pour interpréter les coefficients, on peut revenir aux odds ratios. Par exemple si on regarde l’odds de petits prix et marque vs la référence pour une femme avec même âge, on peut les calculer avec \(\exp(\theta_1^{(m)})\) :
Enseigne PetitPrix
1.0597023 0.6276534 Une femme a 0.628 fois plus de chances qu’un homme de préférer la marque petit prix à la marque référence.
On peut faire le même travail avec la fonction vglm() de la librairie VGAM. Notons que cette fonction prend la dernière modalité comme référence.
library(VGAM)
D1 <- D
D1[,1] <- factor(D[,1], levels=c("PetitPrix","Enseigne","Reference"))
regMarq2 <- vglm(brand ~ femme + age, data=D1, family=multinomial())
summary(regMarq2)
Call:
vglm(formula = brand ~ femme + age, family = multinomial(), data = D1)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 22.72140 2.05802 11.040 < 2e-16 ***
(Intercept):2 10.94674 1.49316 7.331 2.28e-13 ***
femme1:1 -0.46594 0.22609 -2.061 0.0393 *
femme1:2 0.05787 0.19643 0.295 0.7683
age:1 -0.68591 0.06263 -10.952 < 2e-16 ***
age:2 -0.31770 0.04401 -7.219 5.22e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: log(mu[,1]/mu[,3]), log(mu[,2]/mu[,3])
Residual deviance: 1405.941 on 1464 degrees of freedom
Log-likelihood: -702.9707 on 1464 degrees of freedom
Number of Fisher scoring iterations: 5
Warning: Hauck-Donner effect detected in the following estimate(s):
'age:1'
Reference group is level 3 of the response10.7.2 Régression polytomique ordonnée
Dans cette section, on suppose que \(Y\) est une variable qualitative ordinale, c’est-à-dire que \(Y\) admet \(M\) modalités ordonnées \(u_1 \prec u_2\prec \ldots \prec u_M.\) Par exemple, si on s’intéresse au degré de satisfaction pour un produit (mauvais, moyen, bon, très bon); pour le stade d’évolution d’une maladie; etc. On va illustrer cette section avec le jeu de données suivant : on s’intéresse à la qualité de 34 vins selon l’ensoleillement et la pluviométrie (les variables explicatives sont centrées réduites).
SunRain <- read.table("Data/SunRain.csv", header=T, sep=";")
SunRain[,"Quality"] <- factor(SunRain[,"Quality"], levels=c("bad","medium","good"))
#centre-reduit les variables Sun et Rain
SunRain[,"Sun"] <- (SunRain[,"Sun"] - mean(SunRain[,"Sun"])) / sd(SunRain[,"Sun"])
SunRain[,"Rain"] <- (SunRain[,"Rain"] - mean(SunRain[,"Rain"])) / sd(SunRain[,"Rain"])
attach(SunRain)Un résumé graphique des données est donné en Figure ??.
Sous R, les fonctions polr() et vglm() des librairies MASS et VGAM permettent d’ajuster des modèles de régression polytomique ordonnée.
10.7.2.1 Modélisation par les logits cumulatifs
Pour la modélisation, on suppose qu’il existe une variable latente \(Z\) telle que
- \(Y\) s’écrit à partir de \(Z\) sous la forme suivante \[ Y = \left\{\begin{array}{l l l } u_1 & \textrm{ si } & Z\in\ ]a_0,a_1]\\ u_2 & \textrm{ si } & Z\in\ ]a_1,a_2]\\ \ldots\\ u_M & \textrm{ si } & Z\in\ ]a_{M-1},a_M] \end{array}\right. \] avec \(-\infty = a_0 < a_1 < \ldots < a_{M-1} < a_M=+\infty\) (\(M-1\) coefficients inconnus),
- une liaison linéaire entre \(Z\) et les \(x^{(1)},\ldots,x^{(p)}\) : \[ Z = \beta_1 x^{(1)} + \ldots + \beta_p x^{(p)} + \gamma, \] où \((\beta_1,\ldots,\beta_p)\) sont des paramètres inconnus et \(\gamma\) est une variable aléatoire symétrique de fonction de répartition \(F_\gamma\).
Le modèle de régression polytomique ordonnée revient alors à modéliser pour tout \(m\in\{1,\ldots,M-1\}\), \[ \mathbb{P}(Y \leq u_m | {\bf x}) = \mathbb{P}(Z\leq a_m | {\bf x}) = F_\gamma(a_m - [\beta_1 x^{(1)} + \ldots + \beta_p x^{(p)}]) = F_\gamma({\bf x}\theta^{(m)}), \] avec \({\bf x}=(1,x^{(1)},\ldots,x^{(p)})\) et \(\theta^{(m)}=(a_m,-\beta_1,\ldots,-\beta_p)'\).
Comme dans le cadre binaire, il faut alors choisir une fonction de répartition \(F_\gamma\). Si \(\gamma\) est supposée suivre une loi logistique, on modélise les logits cumulatifs par \[\textrm{logit}\left[ \mathbb{P}(Y \leq u_m | {\bf x}) \right] = {\bf x}\theta^{(m)} = \theta_0^{(m)} + \theta_1 x^{(1)} + \ldots + \theta_p x^{(p)},\] avec \[\begin{eqnarray*} \textrm{logit}\left[ \mathbb{P}(Y \leq u_m | {\bf x}) \right] &=& \ln\left[\frac{\mathbb{P}(Y \leq u_m | {\bf x})}{\mathbb{P}(Y > u_m | {\bf x})}\right]\\ &=& \ln\left[\frac{\pi_1({\bf x}) + \ldots+\pi_m({\bf x})}{\pi_{m+1}({\bf x}) + \ldots+\pi_M({\bf x})}\right]. \end{eqnarray*}\]
Dans ce modèle, les coefficients des variables explicatives sont identiques et seules les constantes (intercepts) diffèrent selon les modalités de \(Y\). Ainsi, quelque soit la modalité \(u_m\) considérée, une variable explicative donnée a la même influence sur \(\mathbb{P}(Y\leq u_m|{\bf x})\). On dit qu’il y a égalité des pentes. Pour estimer les \(M-1+p\) paramètres, on cherche à maximiser la vraisemblance.
library(VGAM)
levels(SunRain[,"Quality"])<-c("1","2","3")
SunRain[,"Quality"]<-as.numeric(SunRain[,"Quality"])
modelecumulsimpl <- vglm(Quality ~ Sun + Rain, data=SunRain,
family = cumulative(parallel=T,reverse=F))
modelecumulsimpl
Call:
vglm(formula = Quality ~ Sun + Rain, family = cumulative(parallel = T,
reverse = F), data = SunRain)
Coefficients:
(Intercept):1 (Intercept):2 Sun Rain
-1.420824 2.317790 -3.265814 1.588428
Degrees of Freedom: 68 Total; 64 Residual
Residual deviance: 34.50584
Log-likelihood: -17.25292 On peut généraliser ce modèle en supposant que le rôle des variables dépend du niveau de la réponse, en posant \[ \textrm{logit}\left[ \mathbb{P}(Y \leq u_m | {\bf x}) \right] = \theta_0^{(m)} + \theta_1^{(m)} x^{(1)} + \ldots + \theta_p^{(m)} x^{(p)} = {\bf x} \theta^{(m)} \] avec \(\theta^{(m)}=(\theta_0^{(m)} ,\theta_1^{(m)} ,\ldots, \theta_p^{(m)})\). On se retrouve donc avec un modèle à \((M-1)(p+1)\) paramètres (estimés par maximum de vraisemblance).
modelecumul <- vglm(Quality ~ Sun + Rain, data = SunRain,
family = cumulative(parallel=F,reverse=F))
modelecumul
Call:
vglm(formula = Quality ~ Sun + Rain, family = cumulative(parallel = F,
reverse = F), data = SunRain)
Coefficients:
(Intercept):1 (Intercept):2 Sun:1 Sun:2 Rain:1
-1.739086 2.005517 -4.020702 -2.814860 1.795255
Rain:2
1.326761
Degrees of Freedom: 68 Total; 62 Residual
Residual deviance: 34.02694
Log-likelihood: -17.01347 Pour la suite, on va exploiter les résultats de la modélisation simplifiée pour les illustrations. Avec modelecumulsimpl@predictors, on récupère les valeurs des \(\textrm{logit}\left[ \mathbb{P}(Y \leq u_m | {\bf x}) \right]\).
On peut facilement ensuite calculer les probabilités suivantes :
\[
\left\{
\begin{array}{l}
\displaystyle \mathbb{P}(Y \leq u_m | {\bf x}) = \frac{\displaystyle\exp[{\bf x} \theta^{(m)}]}{\displaystyle1 + \exp[{\bf x} \theta^{(m)}]}\\
\displaystyle \mathbb{P}(Y = u_m | {\bf x}) = \mathbb{P}(Y \leq u_m | {\bf x}) - \mathbb{P}(Y \leq u_{m-1} | {\bf x}) \\
\displaystyle \mathbb{P}(Y \leq u_M | {\bf x}) =1.
\end{array}
\right.
\]
probacumul <- exp(modelecumulsimpl@predictors)/(1+exp(modelecumulsimpl@predictors))
head(probacumul) logitlink(P[Y<=1]) logitlink(P[Y<=2])
1 0.9608757 0.9990324
2 0.9994916 0.9999879
3 0.9989072 0.9999740
4 0.9088956 0.9976213
5 0.9995916 0.9999903
6 0.4872894 0.9755831 [,1] [,2] [,3]
1 0.9608757 0.0381566510 9.676064e-04
2 0.9994916 0.0004963458 1.210043e-05
3 0.9989072 0.0010668179 2.602321e-05
4 0.9088956 0.0887257897 2.378656e-03
5 0.9995916 0.0003986827 9.718527e-06
6 0.4872894 0.4882937635 2.441687e-02Dans le cas où \(Y\) est une variable qualitative ordinale, on définit l’odds d’un individu \({\bf x}\) relativement à \(Y\leq u_m\) par \[ \textrm{odds}({\bf x} | u_m) = \frac{\mathbb{P}(Y\leq u_m | {\bf x})}{1-\mathbb{P}(Y\leq u_m | {\bf x})} = \exp[{\bf x} \theta^{(m)}]. \] L’odds ratio entre deux individus \({\bf x}\) et \(\tilde{\bf x}\) relativement à \(Y\leq u_m\) s’écrit alors \[ \textrm{OR}({\bf x},\tilde{\bf x}| u_m) = \frac{\textrm{odds}({\bf x}| u_m) }{\textrm{odds}(\tilde{\bf x}| u_m) } = \exp\left[\sum_{j=1}^p \theta_j^{(m)} (x^{(j)} - \tilde{x}^{(j)})\right] . \] On peut remarquer que cet odds ratio ne dépend pas de \(\theta_0^{(m)}\). Aussi dans le cas de la modélisation avec pentes parallèles, cet odds ratio ne dépend pas de la modalité \(u_m\). En particulier, si \({\bf x}\) et \(\tilde{\bf x}\) ne diffèrent que d’une unité pour seulement une variable \(j\), alors \(\textrm{OR}({\bf x},\tilde{\bf x}| u_m) = \exp[\theta_j^{(m)}]\).
Dans notre exemple, lorsque l’on observe la valeur moyenne des variables explicatives (\({\bf x}=(1,0,0)\) car les données sont centrées), on obtient dans notre exemple que
\(\textrm{odds}({\bf x} | "{\tt bad}") = e^{-1.420} = 0.24\) : on a 0.24 fois plus de chance d’avoir un vin de qualité “bad” que d’une qualité meilleure. De même,
\(\textrm{odds}({\bf x} | "{\tt medium}") = e^{2.317} = 10.15\) : on a 10.15 fois plus de chance d’avoir un vin de qualité inférieure à “medium” que “good”.
Lorsque les jours d’ensoleillement augmentent de 1, on a \(e^{-3.265814} = 0.04\) fois plus de chances d’avoir un vin moins bon qu’il ne l’est.
10.7.2.2 Modélisation par les logits adjacents
Il est également possible de définir la modélisation à partir des logits adjacents : \[ \left\{ \begin{array}{l} L_{M-1} = \ln\left[\frac{\pi_{M}({\bf x})}{\pi_{M-1}({\bf x})}\right] = \theta_0^{(M-1)} + \theta_1^{(M-1)} x^{(1)} + \ldots + \theta_p^{(M-1)} x^{(p)}\\ \ldots\\ L_2 = \ln\left[\frac{\pi_3({\bf x})}{\pi_2({\bf x})}\right] = \theta_0^{(2)} + \theta_1^{(2)} x^{(1)} + \ldots + \theta_p^{(2)} x^{(p)}\\ \\ L_1 = \ln\left[\frac{\pi_2({\bf x})}{\pi_1({\bf x})}\right] = \theta_0^{(1)} + \theta_1^{(1)} x^{(1)} + \ldots + \theta_p^{(1)} x^{(p)}\\ \end{array} \right. \] C’est la même idée que pour la régression multinomiale mais la catégorie de référence change à chaque étape. On peut relier les deux en remarquant que \[ \left\{ \begin{array}{l} \ln\left[\frac{\pi_2({\bf x})}{\pi_1({\bf x})}\right] = L_1 \\ \\ \ln\left[\frac{\pi_3({\bf x})}{\pi_1({\bf x})}\right] = L_2 + L_1\\ \ldots\\ \ln\left[\frac{\pi_M ({\bf x})}{\pi_1({\bf x})}\right] = L_{M_1} + \ldots + L_2 + L_1 \end{array} \right. \]
Comme précédemment, on peut considérer une modélisation simplifiée pour limiter le nombre de paramètres : \[ \ln\left[\frac{\pi_{m+1}({\bf x})}{\pi_{m}({\bf x})}\right] = \theta_0^{(m)} + \theta_1 x^{(1)} + \ldots + \theta_p x^{(p)}. \]
Pour notre exemple, on ajuste le modèle “complet” et le modèle “simplifié” :
modeleadj <- vglm(Quality ~ Sun + Rain, data = SunRain,
family = acat(parallel=F,reverse=F))
summary(modeleadj)
Call:
vglm(formula = Quality ~ Sun + Rain, family = acat(parallel = F,
reverse = F), data = SunRain)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 1.649 1.055 1.564 0.1179
(Intercept):2 -1.700 0.894 -1.901 0.0572 .
Sun:1 4.110 2.010 NA NA
Sun:2 2.504 1.141 2.195 0.0281 *
Rain:1 -1.727 1.052 -1.641 0.1008
Rain:2 -1.185 1.036 -1.144 0.2526
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: loglink(P[Y=2]/P[Y=1]), loglink(P[Y=3]/P[Y=2])
Residual deviance: 33.6889 on 62 degrees of freedom
Log-likelihood: -16.8445 on 62 degrees of freedom
Number of Fisher scoring iterations: 7
Warning: Hauck-Donner effect detected in the following estimate(s):
'Sun:1'modeleadjsimpl <- vglm(Quality ~ Sun + Rain, data = SunRain,
family = acat(parallel=T,reverse=F))
summary(modeleadjsimpl)
Call:
vglm(formula = Quality ~ Sun + Rain, family = acat(parallel = T,
reverse = F), data = SunRain)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 1.2810 0.7439 1.722 0.08506 .
(Intercept):2 -2.0369 0.8481 -2.402 0.01632 *
Sun 3.0711 0.9924 3.095 0.00197 **
Rain -1.4709 0.7037 -2.090 0.03658 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: loglink(P[Y=2]/P[Y=1]), loglink(P[Y=3]/P[Y=2])
Residual deviance: 34.3157 on 64 degrees of freedom
Log-likelihood: -17.1578 on 64 degrees of freedom
Number of Fisher scoring iterations: 7
No Hauck-Donner effect found in any of the estimatesOn définit l’odds d’une modalité \(u_{m+1}\) par rapport à \(u_m\) relativement à un individu \({\bf x}\) par \[ \textrm{odds}(Y=u_{m+1} \mbox{vs }Y=u_m ; {\bf x}) = \frac{\mathbb{P}(Y=u_{m+1} | {\bf x})}{\mathbb{P}(Y=u_{m} | {\bf x})} = \frac{\pi_{m+1}({\bf x})}{\pi_m({\bf x})} = \exp\left[ {\bf x} \theta^{(m)} \right]. \] Pour deux individus \({\bf x}\) et \(\tilde{\bf x}\), on définit alors l’odds ratio par \[\begin{eqnarray*} \textrm{OR}(Y=u_{m+1} \mbox{vs }Y=u_{m} ; {\bf x},\tilde{\bf x}) &=& \frac{\textrm{odds}(Y=u_{m+1} \mbox{vs }Y=u_{m} ; {\bf x})}{\textrm{odds}(Y=u_{m+1} \mbox{vs }Y=u_{m} ; \tilde{\bf x})} \\ &=& \exp\left[ \sum_{j=1}^p (x^{(j)} - \tilde{x}^{(j)} ) \theta_j^{(m)}\right]. \end{eqnarray*}\] Ainsi si les deux individus \({\bf x}\) et \(\tilde{\bf x}\) ne diffèrent que d’une unité pour la variable \(j\), on a \[ \textrm{OR}(Y=u_{m+1} \mbox{vs }Y=u_{m} ; {\bf x},\tilde{\bf x}) = \exp[\theta_j^{(m)}]. \]
Dans notre exemple, en prenant les résultats de la modélisation complète, on peut par exemple remarquer que si l’ensoleillement augmente d’une unité, on a \(e^{4.11}= 60.9\) fois plus de change que le vin soit “medium” que “bad”; et \(e^{2.504}= 12.2\) fois plus de chance que le vin soir “good” que “medium”. Si l’on prend la modélisation simplifiée, on a \(e^{3.0711}= 21.5\) fois plus de chance de passer dans la catégorie supérieure pour la qualité du vin (que l’on ait un vin “bad” ou “medium” présentement). Lorsque l’on observe la valeur moyenne des variables explicatives (\(x=(0,0)\)), on a \(e^{1.281}=3.6\) fois plus de chance d’avoir un vin “médium” que “bad” et \(e^{-2.0369}=0.13\) fois plus de chance d’avoir un vin “good” que un vin “medium”.
Dans modeleadj@predictors, on récupère l’ensemble des valeurs des prédicteurs linéaires \(\ln\left[\hat\pi_{m+1}({\bf x}_i) / \hat \pi_{m}({\bf x}_i)\right]\). A partir de ces valeurs, on peut retrouver les \(\pi_m({\bf x}_i)\) (disponibles dans modeleadj@fitted.values) par la formule
\[
\left\{\begin{array}{l}
\hat \pi_{m+1}({\bf x}) = \frac{\displaystyle \prod_{v=1}^m e^{{\bf x} \hat \theta^{(v)}}}{\displaystyle 1 + \sum_{m'=1}^{M-1}\prod_{v=1}^{m'} e^{{\bf x} \hat \theta^{(v)}}}, \quad \forall m\in\{1,\ldots,M-1\} \\ \\
\hat \pi_{1}({\bf x}) = \frac{\displaystyle 1}{\displaystyle 1 + \sum_{m=1}^{M-1} \prod_{v=1}^{m} e^{{\bf x} \hat\theta^{(v)}}}.
\end{array}\right.
\]
On définit alors les prédictions pour nos \(n\) individus par \[ \hat Y_i = u_{\hat m} \quad\textrm{où}\quad \hat m\in\underset{m=1,\ldots,M}{\mbox{argmax}}\ \hat{\pi}_m({\bf x}_i). \] Dans notre exemple, on compare ainsi les prédiction avec les valeurs observées de la réponse :
hatY
Quality 1 2 3
bad 11 1 0
medium 1 8 2
good 0 3 8